Chuyên đề đồ thị hàm số chứa dấu trị tuyệt đối
Đây là chuyên đề không mới nhưng nó thường gây bối rối và khó khăn cho học sinh. Học sinh sẽ lúng túng khi gặp các hàm số có dấu trị tuyệt đối, không biết tìm cách nào để phá dấu trị tuyệt đối ra hoặc thường mắc sai lầm khi tự nhiên vứt dấu trị tuyệt đối đi mà không xét điều kiện cho nó.
Lý thuyết chung: ![]() .
.
1. Đồ thị hàm số  .
.
Phương pháp: Gọi (C) là đồ thị của hàm số ![]() .
.
Hàm số  .
.
Tức là
- Giữ nguyên phần đồ thị hàm số (C) phía trên trục Ox, đặt là
 .
. - Phần đồ thị (C) phía dưới trục Ox đem lấy đối xứng qua Ox được phần đồ thị mới đặt là
 .
. - Đồ thị hàm số
 là $(C_{1}) \cup (C_{2})$.
là $(C_{1}) \cup (C_{2})$.
Ví dụ: Vẽ đồ thị hàm số ![]() biết đồ thị hàm số $y=x^{3}+3x^{2}-2$ là
biết đồ thị hàm số $y=x^{3}+3x^{2}-2$ là 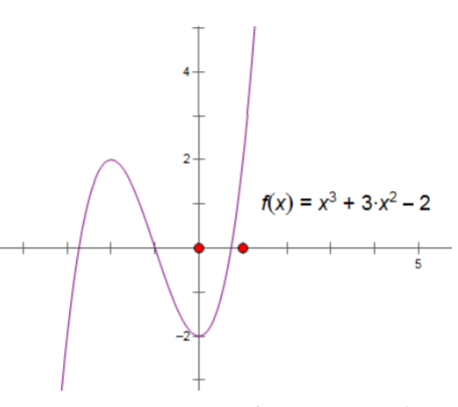
Giải: Ta có ![y=|x^{3}+3x^{2}-2|=\left\{\begin{matrix} x^{3}+3x^{2}-2 \: khi \: x \in [-1-\sqrt{3},-1] \cup [-1+\sqrt{3}, +\infty) \\ -(x^{3}+3x^{2}-2) \: khi \: x \in (-\infty, -1-\sqrt{3}) \cup (-1, -1+\sqrt{3})\end{matrix}\right.](https://i.khoahoc.com.vn/data/image/holder.png) .
.
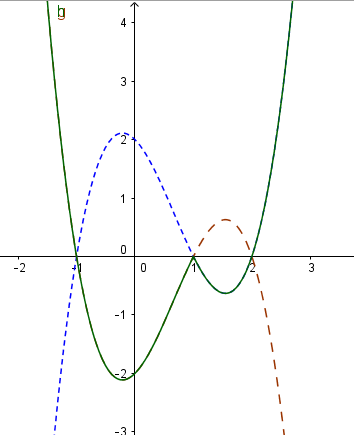
Ta thấy đồ thị hàm số ![]() (màu đỏ) là đồ thị đối xứng của đồ thị $y=x^{3}+3x^{2}-2$ (màu xanh) qua trục Ox.
(màu đỏ) là đồ thị đối xứng của đồ thị $y=x^{3}+3x^{2}-2$ (màu xanh) qua trục Ox.
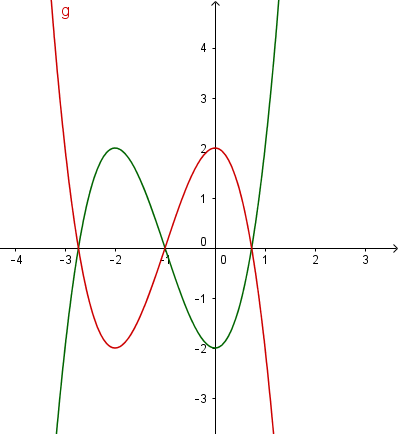
Đồ thị ![]() ta chỉ lấy trong khoảng $ x \in [-1-\sqrt{3},-1] \cup [-1+\sqrt{3}, +\infty)$ và đồ thị $y=-(x^{3}+3x^{2}-2)$ ta lấy trong khoảng $x \in (-\infty, -1-\sqrt{3}) \cup (-1, -1+\sqrt{3})$. Ta có đồ thị hàm số $y=|x^{3}+3x^{2}-2|$ như sau
ta chỉ lấy trong khoảng $ x \in [-1-\sqrt{3},-1] \cup [-1+\sqrt{3}, +\infty)$ và đồ thị $y=-(x^{3}+3x^{2}-2)$ ta lấy trong khoảng $x \in (-\infty, -1-\sqrt{3}) \cup (-1, -1+\sqrt{3})$. Ta có đồ thị hàm số $y=|x^{3}+3x^{2}-2|$ như sau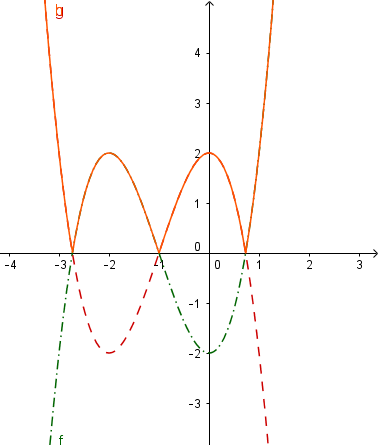 Hay
Hay
- Bước 1: Giữ nguyên phần đồ thị (C) phía trên trục Ox, đặt là


- Bước 2: Phần đồ thị (C) bên dưới trục Ox đem lấy đối xứng qua Ox được phần đồ thị mới đặt
 .
.
Ta có đồ thị hàm số ![]() là $C_{1} \cup C_{2}$.
là $C_{1} \cup C_{2}$.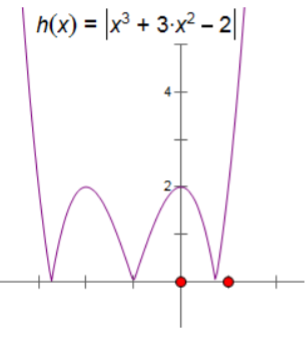
2. Đồ thị hàm số 
Phương pháp: Gọi (C) là đồ thị hàm số ![]() .
.
Ta có 
Tức là
- Bên phải trục Oy giữ nguyên (C) đặt là
 , bỏ phần (C) còn lại.
, bỏ phần (C) còn lại. - Lấy đối xứng với
 ở trên qua Oy được $(C_{2})$.
ở trên qua Oy được $(C_{2})$. - Đồ thị hàm số
 là $(C_{1}) \cup (C_{2})$
là $(C_{1}) \cup (C_{2})$
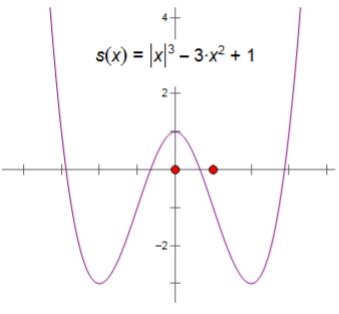
Ví dụ: Vẽ đồ thị hàm số ![]() biết đồ thị hàm số $y=x^{3}-3x^{2}+1$ là
biết đồ thị hàm số $y=x^{3}-3x^{2}+1$ là
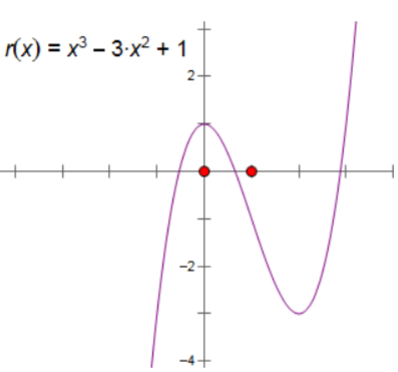
Giải:

Ta thấy đồ thị hàm số ![]() (màu đen) là đồ thị đối xứng của đồ thị hàm số $y=x^{3}-3x^{2}+1$ (màu nâu) qua trục Oy.
(màu đen) là đồ thị đối xứng của đồ thị hàm số $y=x^{3}-3x^{2}+1$ (màu nâu) qua trục Oy.
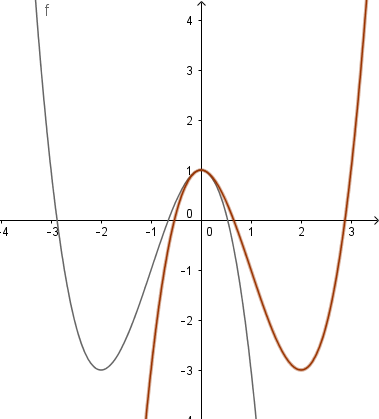
Đồ thị hàm số ![]() lấy trong khoảng $x \geq 0$ và đồ thị hàm số $y=-x^{3}-3x^{2}+1$ lấy trong khoảng x
lấy trong khoảng $x \geq 0$ và đồ thị hàm số $y=-x^{3}-3x^{2}+1$ lấy trong khoảng x

Hay
- Bước 1: Giữ nguyên phần đồ thị bên phải trục tung của đồ thị hàm số (C) ta đặt là
 .
.
- Bước 2: Lấy đối xứng với
 ở trên qua trục Oy được đồ thị $(C_{2})$.
ở trên qua trục Oy được đồ thị $(C_{2})$.
- Đồ thị hàm số
 là $(C_{1}) \cup (C_{2})$
là $(C_{1}) \cup (C_{2})$
3. Đồ thị hàm số 
Ta có  .
.
Phương pháp:
- Bước 1: Vẽ đồ thị hàm số
 .
. - Bước 2: Lấy đối xứng đồ thị hàm số
 qua trục Ox ta được đồ thị hàm số $y=-f(x)g(x)$.
qua trục Ox ta được đồ thị hàm số $y=-f(x)g(x)$. - Bước 3: Đồ thị hàm số cần tìm là phần đồ thị hàm số
 khi $f(x) \geq 0$ và phần đồ thị hàm số $y=-f(x).g(x)$ khi $f(x)
khi $f(x) \geq 0$ và phần đồ thị hàm số $y=-f(x).g(x)$ khi $f(x)
Ví dụ: Vẽ đồ thị hàm số ![]() .
.
Giải: 
Đồ thị hàm số ![]()
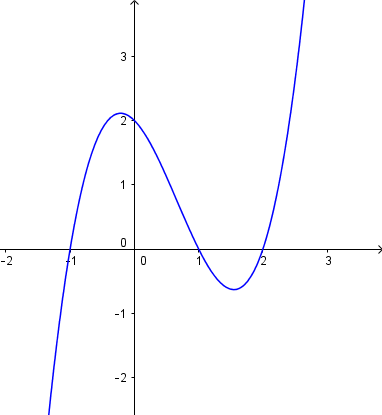
Đồ thị hàm số ![]() là đối xứng của đồ thị hàm số $y=-(x^{3}-2x^{2}-x+2$.
là đối xứng của đồ thị hàm số $y=-(x^{3}-2x^{2}-x+2$.

Đồ thị hàm số ![]() lấy trong khoảng $x \geq 1$ và đồ thị hàm số $y=-(x^{3}-2x^{2}-x+2$ lấy trong khoảng $x
lấy trong khoảng $x \geq 1$ và đồ thị hàm số $y=-(x^{3}-2x^{2}-x+2$ lấy trong khoảng $x
B. BÀI TẬP VÀ HƯỚNG DẪN GIẢI
Kiến thức thú vị
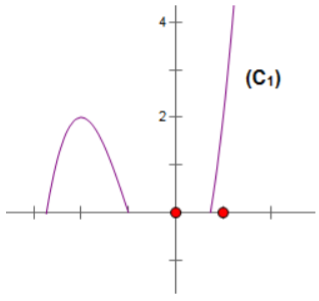
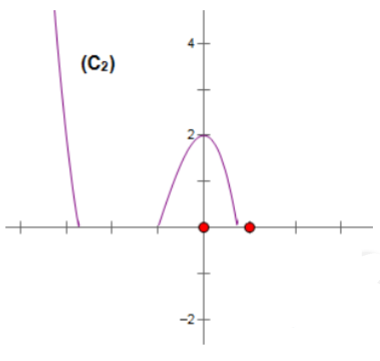
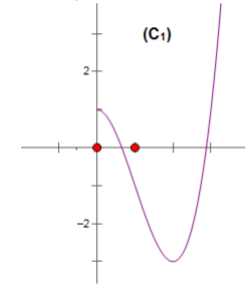
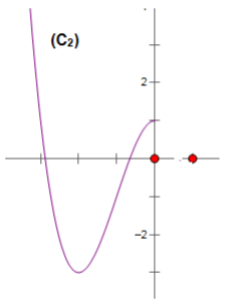
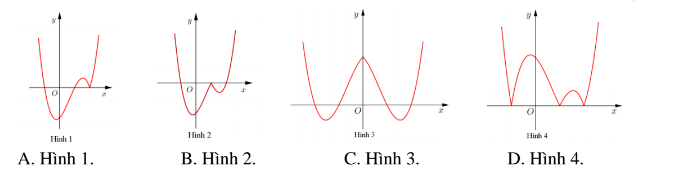
Câu 1(Đề minh họa của Bộ lần 3): Hàm số ![]() có đồ thị như hình bên. Hình nào dưới đây là đồ thị của hàm số $y=|x-2|(x^{2}-1)$?
có đồ thị như hình bên. Hình nào dưới đây là đồ thị của hàm số $y=|x-2|(x^{2}-1)$?
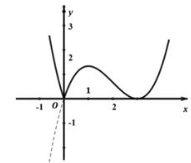
Câu 2: Đồ thị hình bên là của hàm số nào?
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
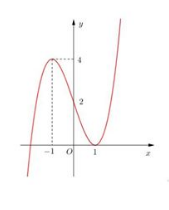
Câu 3: Cho hàm số ![]() có đồ thị như hình vẽ ở bên. Tìm tập hợp tất cả các giá trị của m để đồ thị hàm số $y=f(|x|+m)$ có 5 điểm cực trị
có đồ thị như hình vẽ ở bên. Tìm tập hợp tất cả các giá trị của m để đồ thị hàm số $y=f(|x|+m)$ có 5 điểm cực trị
A. m>1.
B. m>-1.
C. m <-1.
D. m<1