Phương trình đường thẳng trong không gian Toán 12

1 Đánh giá

Giải bài 3: Phương trình đường thẳng trong không gian được Khoahoc sưu tầm và đăng tải. Phương trình đường thẳng trong không gian. Một kiến thức mới đòi hỏi các bạn em sinh cần nắm được lý thuyết để vận dụng giải quyết các bài toán. Dưới đây là phần nội dung tóm tắt kiến thức cũng như hướng dẫn giải các bài tập một cách chi tiết, dễ hiểu, giúp các em nắm bài tốt hơn.

Bài 3: Phương trình đường thẳng trong không gian

A. Tổng hợp kiến thức
- I. Phương trình tham số của đường thẳng
- II. Điều kiện để hai đường thẳng song song, cắt nhau, chéo nhau
B. Bài tập và hướng dẫn giải
Kiến thức thú vị
Phần tham khảo mở rộng
- Dạng 1: Vết phương trình đường thẳng d đi qua A và vuông góc với hai đường thẳng và .

A. Tổng hợp kiến thức

I. Phương trình tham số của đường thẳng

Định lí

Trong không gian Oxyz cho đường thẳng $\Delta$ đi qua điểm $M_{0}(x_{0};y_{0};z_{0})\ và\ nhận\ \overrightarrow{a}=(a_{1},a_{2};a_{3})$ làm vectơ chỉ phương.
Điều kiện cần và đủ để điểm $M(x;y;z)$ nằm trên $\Delta$ là có một số thực t sao cho:

$\left\{\begin{matrix}x=x_{0}+ta_{1} & & \\ y=y_{0}+ta_{2} & & \\ z=z_{0}+ta_{3} & & \end{matrix}\right.$

II. Điều kiện để hai đường thẳng song song, cắt nhau, chéo nhau

1. Hai đường thẳng song song

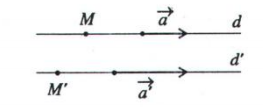
Bài 3: Phương trình đường thẳng trong không gian

d // d' <=> $d//d'<=>\left\{\begin{matrix}\overrightarrow{a}=k\overrightarrow{a'} & & \\ M \in d & & \\ M \notin d' & & \end{matrix}\right.$ </=>
$d \equiv d'<=>\left\{\begin{matrix}\overrightarrow{a}=k\overrightarrow{a'} & & \\ M \in d & & \\ M \in d' & & \end{matrix}\right.$

2. Hai đường thẳng cắt nhau

Cho d: $\left\{\begin{matrix}x=x_{0}+ta_{1} & & \\ y=y_{0}+ta_{2} & & \\ z=z_{0}+ta_{3} & & \end{matrix}\right.$ và d': $\left\{\begin{matrix}x=x_{0}'+t'a_{1}' & & \\ y=y_{0}'+t'a_{2}' & & \\ z=z_{0}'+t'a_{3}' & & \end{matrix}\right.$

$d$ và d' cắt nhau <=> $\left\{\begin{matrix}x_{0}+ta_{1}=x_{0}'+t'a_{1}' & & \\ y_{0}+ta_{2}=y_{0}'+t'a_{2}' & & \\ z_{0}+ta_{3}=z_{0}'+t'a_{3}' & & \end{matrix}\right.$ có đúng một nghiệm.</=>

3. Hai đường thẳng chéo nhau

$d$ và d' chéo nhau <=> $\left\{\begin{matrix}x_{0}+ta_{1}=x_{0}'+t'a_{1}' & & \\ y_{0}+ta_{2}=y_{0}'+t'a_{2}' & & \\ z_{0}+ta_{3}=z_{0}'+t'a_{3}' & & \end{matrix}\right.$ vô nghiệm.</=>

B. Bài tập và hướng dẫn giải

Câu 1: Trang 89 - sgk hình học 12

Viết phương trình tham số của đường thẳng d trong các trường hợp sau:

a) d đi qua điểm M(5 ; 4 ; 1) có vec tơ chỉ phương $\overrightarrow{a}=(2;-3;1)$

b) d đi qua điểm A(2 ; -1 ; 3) và vuông góc với mặt phẳng ( $\alpha$ ) có phương trình: x + y - z + 5 = 0

c) d đi qua điểm B(2 ; 0 ; -3) và song song với đường thẳng ∆ có phương trình: $\left\{\begin{matrix}x=1+2t & & \\y=-3+3t & & \\ z=4t & & \end{matrix}\right.$

d) d đi qua hai điểm P(1; 2; 3) và Q(5; 4; 4).

=> Xem hướng dẫn giải

Câu 2: Trang 89 - sgk hình học 12

Viết phương trình tham số của đường thẳng là hình chiếu vuông góc của đường thẳng

d: $\left\{\begin{matrix}x=2+t & & \\y=-3+2t & & \\ z=1+3t & & \end{matrix}\right.(t \in R)$ lần lượt trên các mặt phẳng sau:

a) (Oxy)

b) (Oyz)

=> Xem hướng dẫn giải

Câu 3: Trang 90 sgk hình học 12

Xét vị trí tương đối của đường thẳng d và d' trong các trường hợp sau:

a) d: $\left\{\begin{matrix}x=-3+2t & & \\y=-2+3t & & \\ z=6+4t & & \end{matrix}\right.$ và d': $\left\{\begin{matrix}x=5+t' & & \\y=-1-4t' & & \\ z=20+t' & &\end{matrix}\right.$

b) $\left\{\begin{matrix}x=1+t & & \\y=2+t & & \\ z=3-t & & \end{matrix}\right.$ và $d': \left\{\begin{matrix}x=1+2t' & & \\y=-1+2t' & & \\ z=2-2t' & & \end{matrix}\right.$

=> Xem hướng dẫn giải

Câu 4: Trang 90 - sgk hình học 12

Tìm a để hai đường thẳng sau đây cắt nhau:

d: $\left\{\begin{matrix}x=1+at & & \\y=t & & \\ z=-1+2t & & \end{matrix}\right.$ và $d': \left\{\begin{matrix}x=1-t' & & \\y=2+2t' & & \\ z=3-t' & & \end{matrix}\right.$

=> Xem hướng dẫn giải

Câu 5: Trang 90 - sgk hình học 12

Xét vị trí tương đối của đường thẳng d với mặt phẳng ( $\alpha$ ) trong các trường hợp sau:

a) d: $\left\{\begin{matrix}x=12+4t & & \\y=9+3t & & \\ z=1+t & & \end{matrix}\right.$ và $(\alpha): 3x+5y-z-2=0$

b) d: $\left\{\begin{matrix}x=1+t & & \\y=2-t & & \\ z=1+2t & & \end{matrix}\right.$ và $(\alpha): x+3y+z+1=0$

c) d: $\left\{\begin{matrix}x=12+4t & & \\y=1+2t & & \\ z=2-3t & & \end{matrix}\right.$ và $(\alpha): x+y+z-4=0$

=> Xem hướng dẫn giải

Câu 6: Trang 90 - sgk hình học 12

Tính khoảng cách giữa đường thẳng

∆ : $\left\{\begin{matrix}x=-3+2t & & \\y=-1+3t & & \\ z=-1+2t & & \end{matrix}\right.$ và $mp(\alpha): 2x-2y+z+3=0$

=> Xem hướng dẫn giải

Câu 7: Trang 91 - sgk hình học 12

Cho điểm A(1 ; 0 ; 0) và đường thẳng ∆: $\left\{\begin{matrix}x=2+t & & \\y=1+2t & & \\ z=t & & \end{matrix}\right.$

a) Tìm tọa độ điểm H là hình chiếu vuông góc của điểm A trên đường thẳng ∆.

b) Tìm tọa độ điểm A' đối xứng với A qua đường thẳng ∆.

=> Xem hướng dẫn giải

Câu 8: Trang 91 - sgk hình học 12

Cho điểm M(1; 4; 2) và mặt phẳng ( $\alpha$ ): x + y + z – 1 = 0

a)Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M trên mặt phẳng ( $\alpha$ ).

b)Tìm tọa độ điểm M' đối xứng với M qua mặt phẳng ( $\alpha$ ).

c) Tính khoảng cách từ điểm M đến mặt phẳng ( $\alpha$ ).

=> Xem hướng dẫn giải

Câu 9: Trang 91 - sgk hình học 12

Cho hai đường thẳng:

d: $\left\{\begin{matrix}x=1-t & & \\y=2+2t & & \\ z=3t & & \end{matrix}\right.$ và d': $\left\{\begin{matrix}x=1+t & & \\y=3-2t & & \\ z=1 & & \end{matrix}\right.$

Chứng minh d và d' chéo nhau.

=> Xem hướng dẫn giải

Câu 10: Trang 91 - sgk hình học 12

Giải bài toán sau đây bằng phương pháp tọa độ. Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 1.

Tính khoảng cách từ đỉnh A đến các mặt phẳng (A'BD) và (B'D'C).

=> Xem hướng dẫn giải

Phần tham khảo mở rộng

Dạng 1: Vết phương trình đường thẳng d đi qua A và vuông góc với hai đường thẳng $d_{1}$ và $d_{2}$ .

=> Xem hướng dẫn giải

Dạng 2: Viết phương trình đường thẳng d là giao tuyến của hai mặt phẳng $(P): Ax+By+Cz+D=0,(Q): A^{'}x+B^{'}y+C^{'}z+D^{'}=0$

=> Xem hướng dẫn giải

Dạng 3: Viết phương trình hình chiếu của đường thẳng (d) lên mặt phẳng (P).

=> Xem hướng dẫn giải

Dạng 4: Viết phương trình đường thẳng d đi qua điểm A, vuông góc với đường thẳng $d_{1}$ và cắt đường thẳng d_{2}

=> Xem hướng dẫn giải

=> Trắc nghiệm hình học 12 bài 3: Phương trình đường thẳng trong không gian

Giải bài 3: Phương trình đường thẳng trong không gian được Khoahoc chia sẻ trên đây. Hy vọng với tài liệu này sẽ giúp các em nắm chắc nội dung của bài, qua đó chuẩn bị tốt cho bài giảng sắp tới. Chúc các em học tốt, ngoài ra các em có thể thêm các môn học khác có tại, tài liệu học tập lớp 12 này nhé.

32 lượt xem

Xem thêm bài viết khác

Xem thêm Hình học 12

Chủ đề liên quan

Giải toán 12

Phương trình đường thẳng trong không gian Toán 12

Bài 3: Phương trình đường thẳng trong không gian

A. Tổng hợp kiến thức

I. Phương trình tham số của đường thẳng

II. Điều kiện để hai đường thẳng song song, cắt nhau, chéo nhau

B. Bài tập và hướng dẫn giải

Kiến thức thú vị

Phần tham khảo mở rộng

Dạng 1: Vết phương trình đường thẳng d đi qua A và vuông góc với hai đường thẳng và .

Xem thêm bài viết khác

Dạng 1: Vết phương trình đường thẳng d đi qua A và vuông góc với hai đường thẳng $d_{1}$ và $d_{2}$ .