Chuyên đề một số công thức tính nhanh bán kính mặt cầu ngoại tiếp hình chóp
Đây là một chuyên đề khá khó trong phần hình không gian đòi hỏi các bạn phải xác định được tâm của mặt cầu từ đó xác định bán kính của mặt cầu trên.
Phương pháp chung:
- Bước 1: Xác định tâm của đáy từ đó dựng đường thẳng d vuông góc với mặt đáy.
- Bước 2: Dựng mặt phẳng trung trực (P) của cạnh bên bất kì.
- Bước 3: Tâm của mặt cầu là giao điểm của d và (P).
Dạng 1: Hình chóp đều.
Gọi h là chiều cao của hình chóp, a là độ dài cạnh bên của hình chóp. Ta có
|
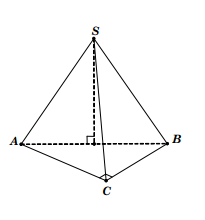
Ví dụ 1: Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh bên bằng 
. Tính bán kính mặt cầu ngoại tiếp khối chóp đã cho.
Giải: Gọi O là tâm của tam giác ABC, suy ra .
Tam giác SOA vuông tại O nên .
Áp dụng công thức .
Bài tập áp dụng
Câu 1: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên bằng 3a. Tính bán kính mặt cầu ngoại tiếp khối chóp đã cho.
Dạng 2: Hình chóp có cạnh bên vuông góc với mặt đáy.
Gọi h, r là chiều cao và bán kính đường tròn ngoại tiếp đa giác đáy. Ta có
|
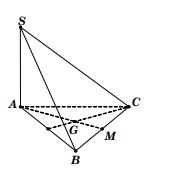Ví dụ 2: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Cạnh bên và vuông góc với đáy (ABC). Tính bán kính mặt cầu ngoại tiếp khối chóp S.ABC.
Giải: Bán kính đường tròn ngoại tiếp tam giác ABC:
, h=SA=a.
Áp dụng công thức, ta có .
Bài tập áp dụng
Câu 2: Cho tứ diện OABC có các cạnh OA, OB, OC đôi một vuông góc với nhau và OA=a, OB=2a, OC=2a. Tính bán kính mặt cầu ngoại tiếp tứ diện OABC.
Câu 3: Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A, AB=a và . Cạnh bên SA=2a và vuông góc với đáy (ABC). Tính bán kính mặt cầu ngoại tiếp hình chóp đã cho.
Câu 4: Cho hình chóp SABCD có đáy ABCD là hình vuông. SA vuông góc với mặt phẳng (ABCD) và SC=2a. Tính bán kính mặt cầu ngoại tiếp hình chóp trên.
Dạng 3: Hình chóp có mặt bên vuông góc với đáy
Gọi Ta có
|
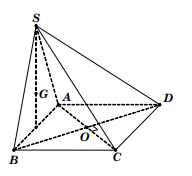Ví dụ 3: Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính bán kính mặt cầu ngoại tiếp hình chóp SABCD.
Giải: Giao tuyến của (SAB) với (ABCD) là AB.
Bán kính đường tròn ngoại tiếp đáy .
Bán kính đường tròn ngoại tiếp mặt bên .
Áp dụng công thức .
Bài tập áp dụng:
Câu 5: Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại B, AB=. Cạnh bên $SA=a \sqrt{2}$, hình chiếu vuông góc với mặt phẳng đáy trùng với trung điểm của cạnh huyền AC. Tính bán kính mặt cầu ngoại tiếp khối chóp.
Câu 6: Cho hình chóp SABC có đáy ABC là tam giác vuông tại C. Mặt phẳng (SAB) vuông góc với đáy, SA=SB=2a, . Tính bán kính mặt cầu ngoại tiếp hình chóp đó.
B. BÀI TẬP VÀ HƯỚNG DẪN GIẢI
Kiến thức thú vị
Câu 1: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên bằng 3a. Tính bán kính mặt cầu ngoại tiếp khối chóp đã cho.
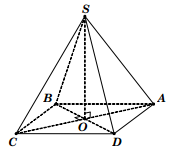
Câu 2: Cho tứ diện OABC có các cạnh OA, OB, OC đôi một vuông góc với nhau và OA=a, OB=2a, OC=2a. Tính bán kính mặt cầu ngoại tiếp tứ diện OABC.
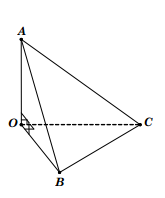
Câu 3: Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A, AB=a và . Cạnh bên SA=2a và vuông góc với đáy (ABC). Tính bán kính mặt cầu ngoại tiếp hình chóp đã cho.
Câu 4: Cho hình chóp SABCD có đáy ABCD là hình vuông. SA vuông góc với mặt phẳng (ABCD) và SC=2a. Tính bán kính mặt cầu ngoại tiếp hình chóp trên.
Câu 5: Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại B, AB=. Cạnh bên $SA=a \sqrt{2}$, hình chiếu vuông góc với mặt phẳng đáy trùng với trung điểm của cạnh huyền AC. Tính bán kính mặt cầu ngoại tiếp khối chóp.
Câu 6: Cho hình chóp SABC có đáy ABC là tam giác vuông tại C. Mặt phẳng (SAB) vuông góc với đáy, SA=SB=a, . Tính bán kính mặt cầu ngoại tiếp hình chóp đó.
Lớp 12