Lời giải câu 5, 6- chuyên đề một số công thức tính nhanh bán kính mặt cầu ngoại tiếp hình chóp

Câu 5: Cho hình chóp SABC có đáy ABC là tam giác vuông cân tại B, AB=. Cạnh bên $SA=a\sqrt{2}$, hình chiếu vuông góc với mặt phẳng đáy trùng với trung điểm của cạnh huyền AC. Tính bán kính mặt cầu ngoại tiếp khối chóp.

Câu 6: Cho hình chóp SABC có đáy ABC là tam giác vuông tại C. Mặt phẳng (SAB) vuông góc với đáy, SA=SB=a, . Tính bán kính mặt cầu ngoại tiếp hình chóp đó.

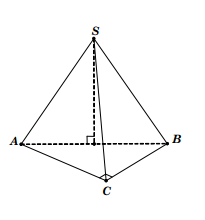
Bài làm:

Câu 5: Gọi M là trung điểm AC, từ giả thiết suy ra .

Tam giác SAC có SM là đường cao và cũng là trung tuyến nên tam giác SAC cân tại S.

Ta có , suy ra tam giác SAC vuông cân tại S $\Rightarrow R_b=a$.

, $GT=AC=2a$.

Áp dụng công thức .

Câu 6: Ta có .

Suy ra , $R_d=\frac{AB}{2}=\frac{a\sqrt{3}}{3}$,

Vậy .