Một số công thức và phương pháp tính nhanh trắc nghiệm- Chuyên đề HÀM SỐ
Trong bài viết này, mình đã sưu tầm và tổng kết lại một số công thức và phương pháp tính nhanh trắc nghiệm trong chuyên đề hàm số.
A. Hàm số ![]() .
.
Bài toán 1: Cho hàm số ![]() . Khi nào hàm số có hai điểm cực trị.
. Khi nào hàm số có hai điểm cực trị.
Phương pháp: ![]()
Để hàm số có cực trị thì phương trình ![]() có hai nghiệm phân biệt $\Leftrightarrow \Delta>0 $ ($\Delta'>0$) hay
có hai nghiệm phân biệt $\Leftrightarrow \Delta>0 $ ($\Delta'>0$) hay
Bài toán 2: Cho hàm số ![]() . Tính khoảng cách giữa hai điểm cực trị.
. Tính khoảng cách giữa hai điểm cực trị.
Phương pháp:
- Bước 1: Tính y', giải phương trình bằng chức năng EQN và lưu hai nghiệm vào ô nhớ A, B bằng cách nhấn SHIFT RCL.
- Bước 2: Tính giá trị cực trị bằng cách nhập hàm số
 vào máy và sử dụng phím CALC để lưu vào ô nhớ C và D.
vào máy và sử dụng phím CALC để lưu vào ô nhớ C và D. - Bước 3: Tính
 hay $d^{2}=(A-B)^{2}+(C-D)^{2}$.
hay $d^{2}=(A-B)^{2}+(C-D)^{2}$.
Ví dụ: Tìm khoảng cách giữa hai điểm cực trị của hàm số ![]()
Giải:

Bài toán 3: Cho hàm số ![]() . Viết phương trình đường thẳng đi qua hai điểm cực trị.
. Viết phương trình đường thẳng đi qua hai điểm cực trị.
Phương pháp:
Cách 1: Gọi ![]() là một điểm cực trị của đồ thị hàm số.
là một điểm cực trị của đồ thị hàm số.
Ta có ![]() .
.
Hơn nữa, ![]()
![]() .
.
Vậy phương trình đường thẳng đi qua hai điểm cực trị là
Cách 2: Tìm hai điểm cực trị và viết phương trình đường thẳng đi qua hai điểm cực trị đó.
- Bước 1: Giải phương trình
 bằng chức năng EQN và lưu vào ô nhớ A, B.
bằng chức năng EQN và lưu vào ô nhớ A, B. - Bước 2: Tính tung độ tương ứng bằng cách nhập hàm và nhấn CALC.
- Bước 3: Giải hệ phương trình tìm các hệ số a và b của đường thẳng

Ví dụ: Viết phương trình đường thẳng đi qua hai điểm cực trị của hàm số ![]() .
.
Giải:
Cách 1: Phương trình đường thẳng đi qua hai điểm cực trị là ![]()
Cách 2:

Bài toán 4: Bài toán về đồng biến, nghịch biến.
Cách 1: Tính y'
Cách 2: Sử dụng máy tính.
Ví dụ 1: Hàm số ![]() đồng biến trên
đồng biến trên
| A. | B. |
| C. | D. |
Cách 1:
 với $\forall x \neq 2$.
với $\forall x \neq 2$.
Vậy hàm số đã cho đồng biến trên khoảng ![]() . Chọn D.
. Chọn D.
Cách 2: Sử dụng trực tiếp Casio để thử đáp án.
Ta có định lí sau: Giả sử hàm số ![]() có đạo hàm trên khoảng $(a,b)$.
có đạo hàm trên khoảng $(a,b)$.
- Nếu
 với mọi $x \in (a,b)$ thì hàm số đồng biến trên khoảng $(a,b)$.
với mọi $x \in (a,b)$ thì hàm số đồng biến trên khoảng $(a,b)$. - Nếu
 với mọi $x \in (a,b)$ thì hàm số nghịch biến trên khoảng $(a,b)$.
với mọi $x \in (a,b)$ thì hàm số nghịch biến trên khoảng $(a,b)$.
![]() Dùng chức năng tính đạo hàm tại một điểm và gán một giá trị $x_{0}$ nằm trong tập xác định cho trước:
Dùng chức năng tính đạo hàm tại một điểm và gán một giá trị $x_{0}$ nằm trong tập xác định cho trước:
- Nếu kết quả S>0 thì hàm số đã cho đồng biến.
- Nếu kết quả S<0 thì hàm số đã cho nghịch biến.
Cụ thể với bài này: Nhấn tổ hợp SHIFT+ tích phân để tính đạo hàm tại một điểm.
Loại đáp án D vì TXĐ ![]() .
.
Nhập

thu được kết quả 6>0 nên loại A.
Nhập
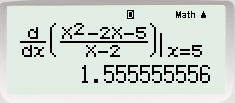
thu được kết quả 1,556>0 nên loại C.
Ví dụ 2: Để hàm số ![]() đồng biến trên $\mathbb{R}$ thì
đồng biến trên $\mathbb{R}$ thì
| A. | B. |
| C. | D. |
Giải:
Bước 1: Nhập dữ liệu với biến x ta gán vào biến X, tham số đi kèm ta gán vào biến Y.
Bước 2: Gán giá trị
- Gán giá trị cho biến X: Ta gán một giá trị nào đó trong tập xác định cho trước.
- Gán giá trị cho biến Y: Chúng ta quan sát vào các đáp án để gán gia trị cho biến Y.
Cụ thể:
- Nhập dữ liệu


- Gán giá trị (ấn nút CALC)
- Vì tập xác định bằng
 nên gán giá trị X=0.
nên gán giá trị X=0.
- Quan sát đáp án thấy m=0 đáp án nào cũng có nên ta không gán
 . Hai đáp án A và C có chiều như nhau. B và D cũng vậy.
. Hai đáp án A và C có chiều như nhau. B và D cũng vậy.
+ Gán ![]() ta có
ta có
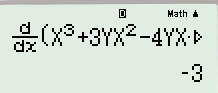
Kết quả <0 nên loại A và C.
+ Gán ![]()

Kết quả > 0 nên loại D.
Ví dụ 3: Hàm số ![]() đồng biến trên $[2,+\infty)$.
đồng biến trên $[2,+\infty)$.
| A. | B. | C. | D. |
Giải:
Đồng biến trên ![]() nên gán $X=2$.
nên gán $X=2$.

Gán ![]() , kết quả >0 thì chỉ có B đúng.
, kết quả >0 thì chỉ có B đúng.

Bài tập áp dụng
Bài 1: Hàm số ![]() đồng biến trên $(1,2)$ khi
đồng biến trên $(1,2)$ khi
| A. | B. | C. | D. |
Bài 2: Hàm số ![]() đồng biến trên khoảng $(2,+\infty)$ khi
đồng biến trên khoảng $(2,+\infty)$ khi
| A. | B. | C. | D. |
Bài toán 5: Bài toán tìm giá trị lớn nhất, giá trị nhỏ nhất.
Phương pháp:
- Nếu hàm số ![]() liên tục trên [a,b] và có đạo hàm trong khoảng (a,b) thì luôn có GTLN, GTNN trên đoạn [a,b] và tìm như sau:
liên tục trên [a,b] và có đạo hàm trong khoảng (a,b) thì luôn có GTLN, GTNN trên đoạn [a,b] và tìm như sau:
- Bước 1: MODE 7
- Bước 2: Nhập hàm
 ấn phím = sau đó nhập Start=a, End=b, Step= $\frac{b-a}{1}$.
ấn phím = sau đó nhập Start=a, End=b, Step= $\frac{b-a}{1}$. - Bước 3: Dựa vào bảng giá trị, tìm GTLN, GTNN của hàm số.
Ví dụ: Giá trị lớn nhất của hàm số ![]() trên đoạn $[-1,1]$ là
trên đoạn $[-1,1]$ là
| A. 40. | B. 21. | C. 50. | D. 35. |
Bước 1: MODE 7
Bước 2: Nhập ![]() ấn phím = sau đó nhập Start=-1. End=1. Step= 0.2
ấn phím = sau đó nhập Start=-1. End=1. Step= 0.2
Bước 3: Tra bảng nhận được và tìm GTLN
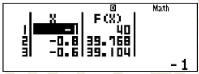
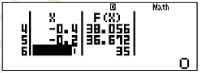

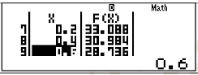
Dựa vào bảng trên, ta thấy GTLN của hàm số là 40.
Chú ý: Cách làm này vẫn đúng khi tìm GTLN và GTNN của một hàm số bất kì trên ![]() .
.
- Tìm GTLN, GTNN của hàm số không cho miền xác định của x.
- Bước 1: Tìm y'
- Bước 2: Tìm nghiệm của phương trình y'=0.
- Bước 3: Tính giá trị của y tại các giá trị của nghiệm trên rồi kết luận.
Bài toán 6: Bài toán tương giao
Phương pháp: Dựa vào đáp án để thử.
Ví dụ: Tìm m để (C): ![]() và $d: y=mx+1$ cắt nhau tại 3 điểm phân biệt.
và $d: y=mx+1$ cắt nhau tại 3 điểm phân biệt.
| A. | B. |
| C. | D. |
Giải: Nhận thấy cả 4 đáp án đều có điều kiện ![]() nên ta bỏ qua điều kiện này trong quá trình thử.
nên ta bỏ qua điều kiện này trong quá trình thử.
- Đầu tiên ta thử với m=5, ta thấy phương trình có 1 nghiệm thực nên loại B, D.
- Thử tiếp với m=0, ta được phương trình có 3 nghiệm thực nên loại C nhận A.












