Giải bài 3: Ứng dụng của tích phân trong hình học
Bài học với nội dung kiến thức về Ứng dụng của tích phân trong hình học. Dựa vào cấu trúc SGK toán lớp 12, KhoaHoc sẽ tóm tắt lại hệ thống lý thuyết và hướng dẫn giải các bài tập 1 cách chi tiết, dễ hiểu. Hi vọng rằng, đây sẽ là tài liệu hữu ích giúp các em học tập tốt hơn
A. Tổng hợp kiến thức
I. Tính diện tích hình phẳng
1. Hình giới hạn bởi một đường cong và trục hoành
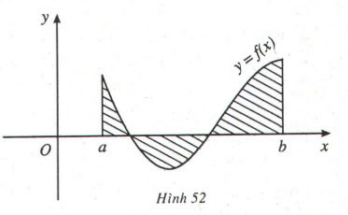
Công thức tổng quát
|
2. Hình giới hạn bởi hai đường cong
Từ hình vẽ:
=> 
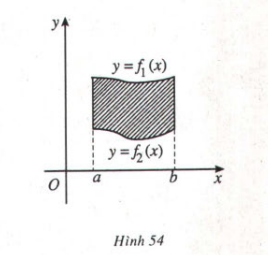
Công thức tổng quát
|
Chú ý:
- Ta có thể chia nhỏ từng khoảng giá trị để tính tích phân, sau đó ghép chúng lại để được kết quả tích phan ban đầu.
|
II. Tính thể tích
1. Thể tích của vật thể
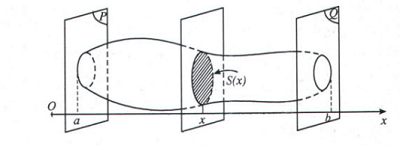
Công thức tổng quát
|
2. Thể tích khối chóp và khối chóp cụt
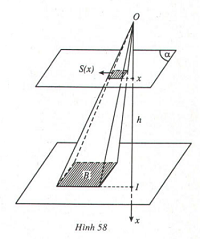
- Với OI = h ( chiều cao)
- B là diện tích đáy.
Ta có:
|
Công thức tổng quát
|
III. Thể tích khối tròn xoay
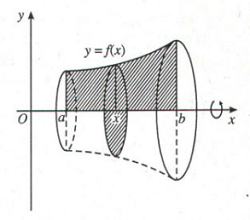Công thức tổng quát
|
B. BÀI TẬP VÀ HƯỚNG DẪN GIẢI
Kiến thức thú vị
Câu 1:Trang 121-sgk giải tích 12
Tính diện tích hình phẳng giới hạn bởi các đường:
a) , $y = x + 2$
b) , $y=1$
c) , $y = 6x– x^{2}$
Câu 2:Trang 121-sgk giải tích 12
Tính diện tích hình phẳng giới hạn bởi đường cong , tiếp tuyến với đường này tại hai điểm M(2; 5) và trục Oy.
Câu 3:Trang 121-sgk giải tích 12
Parabol chia hình tròn có tâm tại gộc toạ độ, bán kính $2\sqrt{2}$ thành hai phần.
Tìm tỉ số diện tích của chúng.
Câu 4:Trang 121-sgk giải tích 12
Tính thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường sau quay quanh trục Ox:
a) ,$y = 0$
b) , $y = 0$, $x = 0$, $x = \prod$
c) , $y = 0$, $x = 0$, $x=\frac{\prod}{4}$
Câu 5:Trang 121-sgk giải tích 12
Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox. Đặt
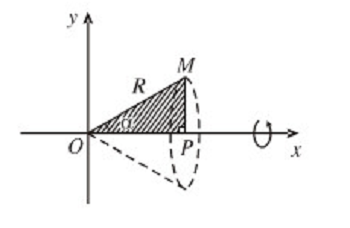
và OM = R ( )
Gọi là khối tròn xoay thu được khi quay tam giác đó xung quanh Ox (H.63).
a) Tính thể tích của theo $\alpha$ và R.
b) Tìm sao cho thể tích $V$ là lớn nhất.
Phần tham khảo mở rộng
Dạng 1: Tính diện tích hình phẳng giới hạn bởi hai đường y=f(x) và y=g(x).
Dạng 2: Tìm thể tích khối tròn xoay được giới hạn bởi đồ thị các hàm số y=f(x), y=g(x), y=h(x).
=> Câu hỏi và bài tập trắc nghiệm toán 12 bài 3: Ứng dụng của tích phân trong hình học
Lớp 12