Giải câu 5 bài: Ứng dụng của tích phân trong hình học

Câu 5:Trang 121-sgk giải tích 12

Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox. Đặt $\widehat{POM}=\alpha$

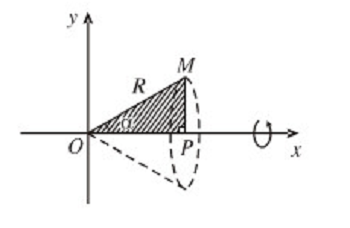
Hướng dẫn giải câu 5 bài Ứng dụng của tích phân trong hình học

và OM = R ( $0\leq \alpha \leq \frac{\prod }{3},R>0$ )

Gọi $v$ là khối tròn xoay thu được khi quay tam giác đó xung quanh Ox (H.63).

a) Tính thể tích của $V$ theo $\alpha$ và R.

b) Tìm $\alpha$ sao cho thể tích $V$ là lớn nhất.

Bài làm:

a) Ta có hoành độ điểm P là: $x_{P} = OP = OM. \cos \alpha = R.\cos \alpha$

=> Phương trình đường thẳng OM là: $y = \ tan \alpha.x$

=> Thể tích của khối tròn xoay là: $V=\prod \int_{0}^{R\cos \alpha }x^{2}\tan ^{\alpha }dx$

<=> $V=\frac{\prod R^{3}}{3}\sin ^{2}\alpha \cos \alpha$

<=> $V=\frac{\prod R^{3}}{3}(\cos \alpha -\cos ^{3}\alpha )$ (đvdt)

Vậy thể tích của khối tròn xoay là: $V=\frac{\prod R^{3}}{3}(\cos \alpha -\cos ^{3}\alpha )$ (đvdt).

b) Ta có: $V'(\alpha )=\frac{\prod R^{3}}{3}(\sin ^{2}\alpha +3\cos ^{2}\alpha \sin \alpha )$

=> $V'(\alpha )=0<=>\frac{\prod R^{3}}{3}(\sin ^{2}\alpha +3\cos ^{2}\alpha \sin \alpha )=0$

<=> $3\cos ^{2}\alpha -1=0$

<=> $\cos \alpha =\frac{1}{\sqrt{3}}$

<=> $\alpha =\arccos (\frac{1}{\sqrt{3}})$

Bảng biến thiên:

Hướng dẫn giải câu 5 bài Ứng dụng của tích phân trong hình học

=> Thể tích $V$ là lớn nhất <=> $\alpha =\arccos (\frac{1}{\sqrt{3}})$.

Cập nhật: 07/09/2021

Xem thêm bài viết khác