Giá trị lớn nhất, giá trị nhỏ nhất của số phức
Phần tham khảo mở rộng
Dạng 1: Giá trị lớn nhất, giá trị nhỏ nhất của số phức
Bài làm:
I. Phương pháp giải:
Chú ý công thức ||z₁| – |z₂|| ≤ |z₁ + z₂| ≤ |z₁ – z₂|.
II. Bài tập áp dụng
Bài tập 1: Cho số phức ![]() thoả mãn $|z-3-4i|=\sqrt{5}.$ Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức $P=|z+2|^2-|z-i|^2.$ Tìm môđun của số phức $w= M+mi$.
thoả mãn $|z-3-4i|=\sqrt{5}.$ Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức $P=|z+2|^2-|z-i|^2.$ Tìm môđun của số phức $w= M+mi$.
Bài giải:
Ta có ![]()
Tính toán ta được ![]() Xét đường thẳng $d: 4x+2y+3-P=0.$
Xét đường thẳng $d: 4x+2y+3-P=0.$
Đường thẳng d và đường tròn (C) có điểm chung khi và chỉ khi
![]()
Vậy ![]() ; $m=13.$ Khi đó $w=33+13i$ nên $|w|=\sqrt{1248}.$
; $m=13.$ Khi đó $w=33+13i$ nên $|w|=\sqrt{1248}.$
Bài tập 2: Cho số phức ![]() thoả mãn $|z^2-2z+5|=|(z-1+2i)(z+3i-1)|$. Tính $\min |w|$ với số phức $w=z-2+2i.$
thoả mãn $|z^2-2z+5|=|(z-1+2i)(z+3i-1)|$. Tính $\min |w|$ với số phức $w=z-2+2i.$
Bài giải:
Ta có ![]()
Khi đó, giả thiết ![]()
![]()
TH1: Với z=1-2i, ta có w=z-2+2i=-1. Vậy ![]() .
.
TH2: Với ![]() (*), đặt z=x+yi, ta có
(*), đặt z=x+yi, ta có
![]()
![]()
Do đó ![]()
Vậy ![]()
Bài tập 3: Cho số phức ![]() thoả mãn $|z|=1.$ Tìm giá trị lớn nhất của biểu thức
thoả mãn $|z|=1.$ Tìm giá trị lớn nhất của biểu thức
![]() .
.
Bài giải:
Gọi ![]()
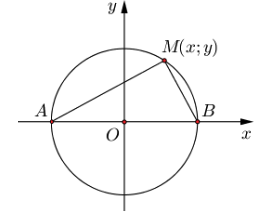
Và ![]() . Ta có $|z|=1 \Rightarrow |x+yi|=1 \Leftrightarrow x^2+y^2=1.$
. Ta có $|z|=1 \Rightarrow |x+yi|=1 \Leftrightarrow x^2+y^2=1.$
![]() thuộc đường tròn đường kính AB.
thuộc đường tròn đường kính AB.
![]() Khi đó, theo Bunhiacopxki, ta có
Khi đó, theo Bunhiacopxki, ta có
![]() .
.
Vậy ![]()
Bài tập 4: Trong các số phức ![]() thoả mãn điều kiện $|z-2-4i|=\sqrt{5}.$ Tìm Max $|z|$; $\min |z|$.
thoả mãn điều kiện $|z-2-4i|=\sqrt{5}.$ Tìm Max $|z|$; $\min |z|$.
Bài giải:
Vì ![]() nên tập hợp các điểm $M(z)$ là đường tròn $(C)$ có tâm $I(2;4)$ và bán kính $R=\sqrt{5}.$
nên tập hợp các điểm $M(z)$ là đường tròn $(C)$ có tâm $I(2;4)$ và bán kính $R=\sqrt{5}.$
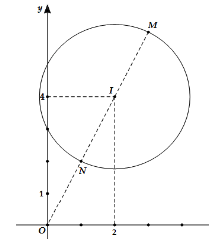
Vậy ![]()
![]()
Bài tập 5: Trong các số phức ![]() thoả mãn điều kiện $|z-5i|\leq 3.$ Tìm số phức có môđun nhỏ nhất.
thoả mãn điều kiện $|z-5i|\leq 3.$ Tìm số phức có môđun nhỏ nhất.
Bài giải:
Tập hợp các điểm ![]() là hình tròn $(C)$ tâm $I(0;5)$ và bán kính R=3.
là hình tròn $(C)$ tâm $I(0;5)$ và bán kính R=3.
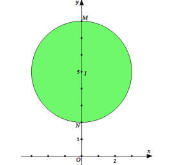
Vậy số phức z có môđun nhỏ nhất là ![]()
Xem thêm bài viết khác
- Giải câu 7 bài: Ôn tập chương 2
- Giải câu 2 bài: Tích phân
- Giải bài 1: Lũy thừa
- Giải bài 4: Phương trình bậc hai với hệ số thực
- Giải câu 4 bài: Lũy thừa
- Giải câu 3 bài: Ứng dụng của tích phân trong hình học
- Giải câu 2 bài 5: Khảo sát sự biến thiên và vẽ đồ thị của hàm số
- Giải câu 2 bài: Lũy thừa
- Giải câu 2 bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
- Tính giá trị biểu thức số phức
- Giải câu 1 bài: Số phức
- Toán 12: Đề kiểm tra học kì 2 dạng trắc nghiệm (Đề 2)











