Giải câu 1 trang 130 toán VNEN 9 tập 1

D. HOẠT ĐỘNG VẬN DỤNG

Câu 1: Trang 130 sách VNEN 9 tập 1

Cho đường tròn (O) có đường kính AB. Từ điểm H nằm trên AB kẻ dây CD vuông góc với AB. Gọi E, F theo thứ tự là hình chiếu của H trên AC, BC. Gọi I, K lần lượt là trung điểm của AH và HB. Vẽ đường tròn (I; IE) và (K; KF).

a) Hãy xác định vị trí tương đối của các đường tròn: (I) và (O), (K) và (O), (I) và (K).

b) Chứng minh rằng EF = HC.

c) Chứng minh rằng CE.CA = CF.CB.

d) Chứng minh rằng EF là tiếp tuyến chung của hai đường tròn (I) và (K).

e) Xác định vị trí của điểm H để EF có độ dài lớn nhất.

f) Cho AH = 4cm, HB = 9cm. Tính diện tích tứ giác IEFK.

A. cm. B. 3cm C. $\frac{2\sqrt{5}}{5}$cm. D. $\sqrt{3}$cm.

Hãy chọn phương án đúng.

Bài làm:

Ta có hình vẽ như sau:

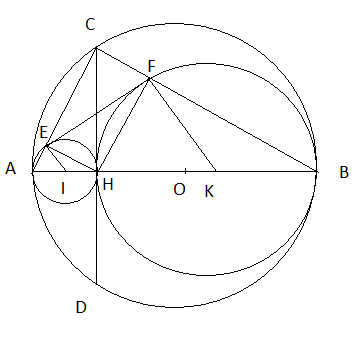
a) (I) và (O) tiếp xúc trong với nhau, (K) và (O) tiếp xúc trong với nhau, (I) và (K) tiếp xúc ngoài với nhau.

b) Tứ giác HECF có = $\widehat{CEF}$ = $\widehat{CFE}$ = $90^{\circ}$ nên tứ giác HECF là hình chữ nhật

EF = CH (hai đường chéo).

c) Ta có: = $\widehat{CHF}$ (do HECF là hình vuông) = $\widehat{CBH}$ (cùng phụ với $\widehat{FHB}$)

Tam giác vuông CEF và tam giác vuông CBA có: = $\widehat{CBH}$ nên tam giác vuông CEF đồng dạng với tam giác vuông CBA

$\frac{CE}{CB}$ = $\frac{CF}{CA}$ CE.CA = CF.CB (đpcm).

d) Tam giác vuông AEH có EI = IH $\widehat{IEH}$ = $\widehat{IHE}$

Mà = $\widehat{ACH}$ (cùng phụ với $\widehat{CAH}$) = $\widehat{EFH}$ (do HECF là hình vuông)

Mặt khác + $\widehat{HEF}$ = $90^{\circ}$ $\Rightarrow $ $\widehat{IEH}$ + $\widehat{HEF}$ = $90^{\circ}$ $\Rightarrow $ $\widehat{IEF}$ = $90^{\circ}$ hay EI $\perp $ EF (1)

Tương tự ta chứng minh được FK EF (2)

Từ (1) và (2) ta được EF là tiếp tuyến chung của (I) và (K).

e) Ta có: EF = CH CO

Suy ra EF lớn nhất khi CH lớn nhất, khi đó CH = CO hay H O

Vậy H O thì EF lớn nhất.

f) EF = CH = = $\sqrt{4.9}$ = 6cm

Diện tích tứ giác IEFK là:

S = .EF = $\frac{2 + 4,5}{2}$.6 = 19,5 $cm^{2}$.