Giải câu 1 trang 83 sách toán VNEN lớp 7 tập 2

C. Hoạt động luyện tập

Câu 1: Trang 83 sách toán VNEN 7 tập 2

Cho tam giác ABC cân tại đỉnh A, trung trực của cạnh AC cắt CB tại điểm D (D nằm ngoài đoạn BC). Trên tia đối tia AD lấy E sao cho AE = BD. Chứng minh tam giác DCE cân. (Gợi ý: Cần chứng minh CD = CE).

Bài làm:

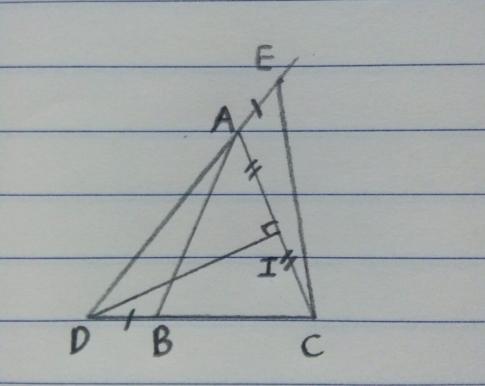
Gọi I là trung điểm của AC

Xét 2 tam giác ADI và CDI, ta có:

- AI = IC

- = $\widehat{CID}$

- DI chung

Suy ra : = $\mathrm{\Delta }CDI$ (c.g.c) => $\widehat{DAI}$ = $\widehat{DCI}$ (cặp góc tương ứng)

Ta có: - + $\widehat{CAE}$ = 180 độ (kề bù)

- + $\widehat{DBA}$ = 180 độ ( vì = $\widehat{ABC}$ ($\mathrm{\Delta }ABC$ cân tại A), mà $\widehat{ABC}$ + $\widehat{ABD}$ = 180 độ (kề bù))

Lại có: Ta có: = $\widehat{DCI}$ (chứng minh trên)

Suy ra: = $\widehat{CAE}$

Xét tam giác ABD và CAE, có:

- DB = EA (gt)

- = $\widehat{CAE}$ (chứng minh trên)

- AB = AC

Suy ra: = $\mathrm{\Delta }CAE$ (c.g.c)

=> AD = CE (1)

mà AD = CD ( = $\mathrm{\Delta }CDI$) (2)

Từ (1) và (2) => DC = CE => Tam giác DCE cân tại C