Giải câu 2 trang 111 toán VNEN 9 tập 1

Câu 2: Trang 111 sách VNEN 9 tập 1

Cho nửa đường tròn (O; R), đường kính AB. Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ là AB). Lấy M trên nửa đường tròn (M A, M B), kẻ tiếp tuyến với nửa đường tròn, nó cắt Ax và By theo thứ tự ở C và D. Chứng minh:

a) Tam giác COD vuông tại O.

b) CD = AC + BD.

c) AC.BD = .

Bài làm:

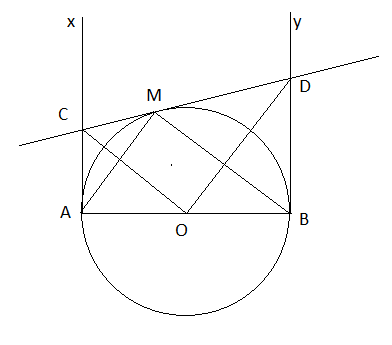
a) Theo tính chất hai tiếp tuyến cắt nhau, ta có: = $\widehat{MCO}$, $\widehat{BDO}$ = $\widehat{MDO}$

$\widehat{MCO}$ + $\widehat{MDO}$ = $\widehat{ACO}$+ $\widehat{BDO}$ = ${90}^{\circ }$

$\widehat{COD}$ = ${90}^{\circ }$

b) Theo tính chất hai tiếp tuyến cắt nhau, ta có: CA = CM, DM = DB

CD = CM + DM = CA + DB (đpcm).

c) Vì MC là tiếp tuyến của đường tròn (O) tại M nên OM CD

Áp dụng hệ thức lượng vào tam giác vuông COD ta có:

= MC.MD $\iff$ $R^2$ = AC.BD (đpcm).