Giải câu 2 trang 114 toán VNEN 9 tập 1

Câu 2: Trang 114 sách VNEN 9 tập 1

Cho tam giác MNP vuông tại M. Gọi R là bán kính đường tròn ngoại tiếp, r là bán kính đường tròn nội tiếp tam giác MNP.

Chứng minh rằng MN + MP = 2(R + r).

Bài làm:

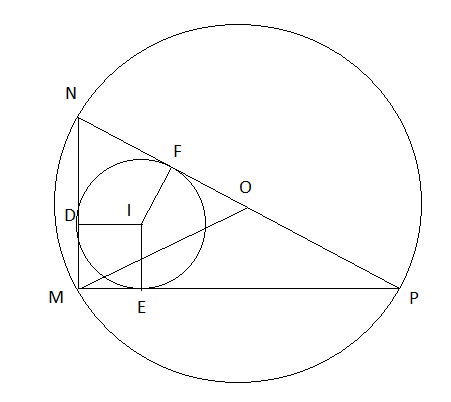
Do tam giác MNP vuông tại M nên NP = 2R

Ta có NM, NP là hai tiếp tuyến của (I) nên theo tính chất tiếp tuyến ta có ND = NF, tương tự ta có PE = PF

Ta có:

MN + MP = MD + DN + ME + EP = MD + ME + NF + PF = MD + ME + NP = r + r + 2R = 2(r + R) (đpcm)

Vậy MN + MP = 2(R + r).