Giải câu 2 trang 56 sách toán VNEN lớp 8 tập 2

Câu 2: Trang 56 sách VNEN 8 tập 2

Tam giác ABC vuông tại A có đường cao AH (H BC). Từ H kẻ HE vuông góc với AB (E AB) và HF vuông góc với AC (F AC). Hỏi khi độ dài các cạnh AB, AC thay đổi thì $\frac{AE}{AB}$ + $\frac{AF}{AC}$ có thay đổi không? Vì sao?

Bài làm:

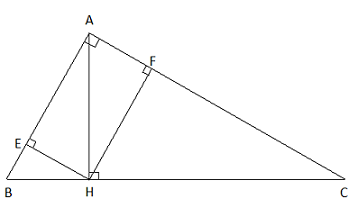
Vì HE AB $\Rightarrow$ HE // AC, theo định lí Ta-lét ta có: $\frac{AE}{AB}$ = $\frac{CH}{CB}$

Vì HF AC $\Rightarrow$ HF // AB, theo định lí Ta-lét ta có: $\frac{AF}{AC}$ = $\frac{BH}{BC}$

$\frac{AE}{AB}$ + $\frac{AF}{AC}$ = $\frac{CH}{CB}$ + $\frac{BH}{BC}$ = $\frac{CH+BH}{CB}$ = $\frac{BC}{BC}$ = 1 (cố định)

Vậy khi độ dài các cạnh AB, AC thay đổi thì + $\frac{AF}{AC}$ không thay đổi