Giải câu 2 trang 96 toán VNEN 9 tập 1

Câu 2: Trang 96 sách VNEN 9 tập 1

a) Cho nửa đường tròn tâm O, đường kính AB. Vẽ dây CD bất kì khác AB. Từ C và D lần lượt kẻ các đường vuông góc với CD, các đường này cắt AB theo thứ tự tại E, F. Chứng minh AF = BE.

b) Cho nửa đường tròn (O), đường kính MN. Trên MN lấy hai điểm A và B sao cho AM = BN. Qua A và B kẻ các đường thẳng song song với nhau, chúng cắt nửa đường tròn (O) lần lượt lại E và F. Chứng minh AE và BF vuông góc với EF.

Bài làm:

a)

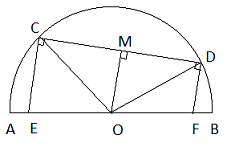
Kẻ OM CD

Xét OCD có OC = OD nên OCD cân tại O, OM $\perp$ CD nên M là trung điểm CD $\Rightarrow$ DM = MC

Ta có: EC//OM//FD (cùng vuông góc với CD)

Theo định lý Ta-lét ta được: = $\frac{FO}{OE}$

Mà DM = MC nên FO = OE

Ta có: OA = OB

OF = OE

suy ra: OA + OF = OB + OE

AF = BE (đpcm).

b)

Kẻ OM // AE // BF (M EF)

Ta có: OM = ON, AM = BN nên OM - AM = OB - BN OA = OB

Theo định lý Ta-lét ta được: = $\frac{BO}{OA}$

Mà OA = OB nên FM = ME hay M là trung điểm EF

Xét OEF có OE = OF, M là trung điểm EF nên OM $\perp$ EF

Mặt khác AE // BF // OM nên AE EF và BF EF (đpcm).