Giải câu 3 trang 112 toán VNEN 9 tập 1

Câu 3: Trang 112 sách VNEN 9 tập 1

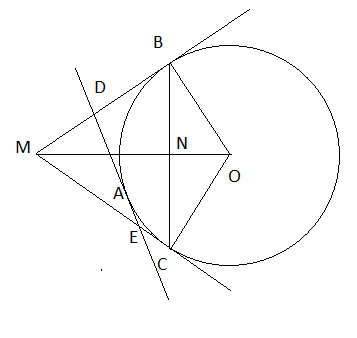
Cho đường tròn (O; 3) và điểm M nằm ngoài đường tròn sao cho Om = 5cm. Kẻ tiếp tuyến MB với đường tròn (O) (B là tiếp điểm). Từ B kẻ đường thẳng vuông gốc MO tại N cắt đường tròn (O) tại C.

a) Chứng minh MC là tiếp tuyến của đường tròn (O).

b) Tính độ dài MN và NO.

c) Qua điểm A trên cung nhỏ BC kẻ tiếp tuyến với đường tròn (O), tiếp tuyến này cắt MB, MC lần lượt tại D và E. Tính chi vi tam giác MED.

d) Tính diện tích tứ giác MBOC.

Bài làm:

a) Xét vuông BNO và vuông CNO có:

ON chung, OB = OC = 3

$\Delta$ BNO = $\Delta $CNO (cạnh huyền, cạnh góc vuông)

BN = NC MO cách đều B, C

MO là phân giác góc MBC

MC là phân giác đường tròn (O) (đpcm).

b) Áp dụng hệ thức lượng trong tam giác vuông MBO, ta có: = ON.OM $\Rightarrow $ ON = $\frac{OB^{2}}{OM}$ =$\frac{3^{2}}{5}$ = $\frac{9}{5}$cm

MN = OM - ON = 5 - $\frac{9}{5}$ = $\frac{16}{5}$cm

c) Theo tính chất hai tiếp tuyến cắt nhau, ta có: DA = DB, EA = EC

Chu vi tam giác MED là:

ME + MD + DE = ME + MD + DA + EA = ME + MD + DB + EC = (MD + DB) + (ME + EC) = MB + MC = 2MB = 2 = 2$\sqrt{5^{2} - 3^{2}}$ = 8cm.

Vậy chu vi tam giác MED là 8cm.

d) SMBOC = SMBO + SMCO = 2MBO (do MBO = MCO) = 2.$\frac{1}{2}$.MB.OB = MB.OB = 4.3 = 12$cm^{2}$

Vậy diện tích tứ giác MBOC là 12.