Giải câu 3 trang 64 toán VNEN 9 tập 1

Câu 3: Trang 64 sách VNEN 9 tập 1

Cho tam giác ABC vuông tại A, phân giác AD. Biết BD = 3 cm; CD = 9$\frac{3}{17}$ cm. Tính độ dài các cạnh góc vuông của tam giác (h.27).

Gợi ý:

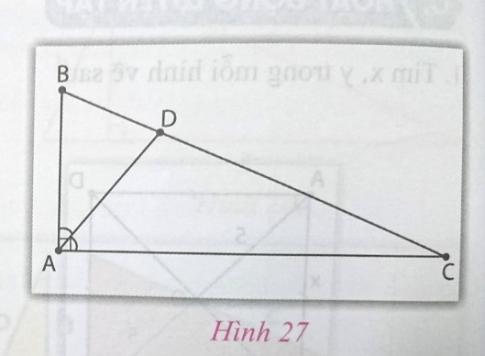
- Tính độ dài BC.

- Sử dụng tính chất đường phân giác: = $\frac{CD}{AC}$ = $\frac{BC}{AB + AC}$.

Bài làm:

Ta có BC = BD + CD = 3 + 9$\frac{3}{17}$ = 13 cm

Theo tính chất đường phân giác ta có:

= $\frac{CD}{AC}$ = $\frac{BC}{AB + AC}$

Xét: = $\frac{CD}{AC}$ $\Leftrightarrow $ BD.AC = CD.AB $\Leftrightarrow $ 3$\frac{14}{17}$.AC = 9$\frac{3}{17}$.AB $\Leftrightarrow $ AC = 2,4AB

Mặt khác tam giác ABC là tam giác vuông nên:

+ $AC^{2}$ = $BC^{2}$ $\Leftrightarrow $ + $(2,4AB)^{2}$ = $13^{2}$ $\Leftrightarrow $ $6,76AB^{2}$ = 169 $\Leftrightarrow $ AB = 5 cm

Suy ra AC = 12cm.