Giải Câu 33 Bài 5: Tính chất tia phân giác của một góc sgk Toán 7 tập 2 Trang 70

Câu 33: Trang 70 - SGK Toán 7 tập 2

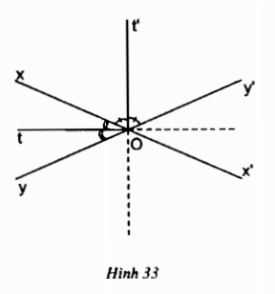
Cho hai đường thẳng xx', yy' cắt nhau tại O.

a) Chứng minh hai tia phân giác Ot, Ot' của một cặp góc kề bù tạo thành một góc vuông.

b) Chứng minh rằng: Nếu M thuộc đường thẳng Ot hoặc thuộc đường thẳng Ot' thì M cách đều hai đường thẳng xx' và yy'.

c) Chứng minh rằng: Nếu điểm M cách đều hai đường thẳng xx', yy' thì M thuộc đường thẳng Ot hoặc thuộc đường thẳng Ot'.

d) Khi M ≡ O thì khoảng cách từ M đến xx' và yy' bằng bao nhiêu?

e) Em có nhận xét gì về tập hợp các điểm cách đều hai đường thẳng cắt nhau xx', yy'.

Bài làm:

a) Vì Ot là phân giác của

nên

Ot' là phân giác của

nên

mà (2 góc kề bù)

=>

Vậy hai tia phân giác của hai góc kề bù tạo thành một góc vuông.

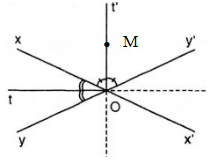
b) Nếu M thuộc Ot hoặc Ot' thì M cách đều hai đường thẳng xx' và yy'

Thật vậy: M Ot do Ot là phân giác của nên M cách đều Ox, Oy.

=> M cách đều xx', yy'

M Ot' do Ot' là phân giác của nên M cách đều xx', yy'.

=> M cách đều xx', yy'.

c) Nếu M cách đều hai đường thẳng xx', yy' và giả sử M nằm trong một góc trong bốn góc , $\widehat{xO{y}^{\prime }}$, $\widehat{x^{\prime }O{y}^{\prime }}$, $\widehat{x^{\prime }Oy}$thì M phải thuộc phân giác của góc ấy. (áp dụng định lí 1)

Tức M phải thuộc Ot hoặc Ot'

d) Khi M ≡ O thì khoảng cách từ M đến xx', yy' bằng 0

e) Từ các câu trên ta có nhận xét: Tập hợp tất cả các điểm cách đều hai đường thẳng cắt nhau xx', yy' thuộc hai đường thẳng vuông góc nhau lần lượt là phân giác của các góc tạo bởi hai đường thẳng cắt nhau đó.