Giải Câu 38 Bài 5: Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn sgk Toán 9 tập 2 Trang 82

Câu 38: Trang 82 – SGK Toán 9 tập 2

Trên một đường tròn, lấy liên tiếp ba cung AC, CD, DB sao cho: sđ cung AC = sđ cung CD = sđ cung DB = . Hai đường thẳng AC, BD cắt nhau tại E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T. Chứng minh rằng

a) = $\widehat{BTC}$

b) CD là tia phân giác của

Bài làm:

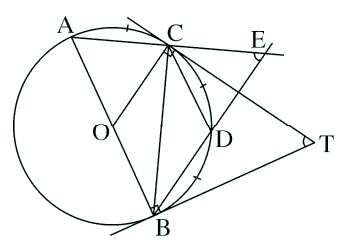
a) Ta có: AB là đường kính của (O) => sđ cung AB =

=> sđ cung lớn BC = sđ cung AB + sđ cung AC =

Sđ cung nhỏ BC = sđ cung CD + sđ cung DB =

Ta có: là góc có đỉnh nằm bên ngoài (O) nên

=$\frac{1}{2}$ . sđ (cung lớn CB – cung nhỏ CB) =$\frac{1}{2}.120^{\circ}$ = $60^{\circ}$ (1)

Mặt khác: là góc có đỉnh nằm bên ngoài (O) nên

=$\frac{1}{2}$ . sđ (cung AB – cung CD) = $\frac{180^{\circ}-60^{\circ}}{2}$ = $60^{\circ}$ (2)

Từ (1)(2) => = $\widehat{AEB}$ (= $60^{\circ}$) (đpcm)

b) Ta có: là góc tạo bởi tia tiếp tiếp CT và dây cung CD của (O) => = $\frac{1}{2}$ . sđ cung CD

Lại có: là góc nội tiếp chắn cung CB của (O) => = $\frac{1}{2}$ . sđ cung CB

mà sđ cung CD = sđ cung CB (gt)

=> = $\widehat{BCD}$

=> CD là tia phân giác của