Giải câu 4 đề 6 ôn thi toán lớp 9 lên 10

Bài 4: (3,5 điểm)

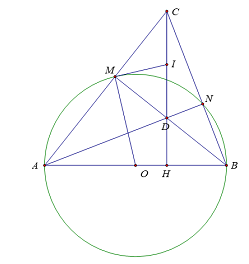
Trên đường tròn (O; R) đường kính AB lấy 2 điểm M, N theo thứ tự A, M, N, B ( hai điểm M, N khác 2 điểm A và B). Các đường thẳng AM và BN cắt nhau tại C, AN và BM cắt nhau tại D

a. Chứng minh tứ giác MCND nội tiếp. Xác định tâm I đường tròn ngoại tiếp tứ giác

b. Gọi H là giao điểm của CD và AB. Chứng minh rằng: BN.BC = BH.BAv

c. Tính ∠IMO

d. Cho biết ∠BAM = ; ∠BAN = $30^{0}$. Tính theo R diện tích của tam giác ABC

Bài làm:

Hình vẽ:

a. Ta có:

∠AMB = (góc nội tiếp chắn nửa đường tròn)

=> ∠DMC =

∠ANB = (góc nội tiếp chắn nửa đường tròn)

=> ∠DNC =

Xét tứ giác MCND có:

∠DMC + ∠DNC = + = $180^{0}$

=> Tứ giác MCDN là tứ giác nội tiếp

Do ∠DMC = nên DC là đường kính đường tròn ngoại tiếp tứ giác MCDN

Do đó tâm I của đường tròn ngoại tiếp tứ giác là trung điểm I của DC

b. Xét tam giác CAB có:

AN ⊥ BC

BM ⊥ AC

AN giao với BM tại H

=> H là trực tâm của tam giác CAB

=> CH ⊥ BA

Xét ΔCHB và ΔBNA có:

∠CBA là góc chung

∠CHB = ∠ANB =

=>ΔCHB ∼ ΔANB

=>=> BN.BC = BA.BH

c. Xét tam giác HDB vuông tại H có:

∠BDH + ∠DBH = (1)

Xét tam giác IDM cân tại I (ID = IM )

=> ∠IMD = ∠IDM

Mà ∠IDM = ∠BDH (đối đỉnh)

=> ∠IMD = ∠BDH (2)

Mặt khác tam giác OBM cân tại O ( OB = OM)

=> ∠OMB = ∠DBH (3)

Từ (1); (2) và (3)

=> ∠IMD + ∠OMB = ∠BDH + ∠DBH =

=> ∠IMO =

d. Xét tam giác BAN vuông tại N có:

∠NAB = => ∠NBA = $60^{0}$

Xét tam giác CHB vuông tại H có ∠NBA =

=>

Lại có: Tam giác CHA vuông tại H có ∠CAH =

=> Tam giác CHA vuông cân tại H => CH = HA

Ta có:

Diện tích tam giác ABC là: