Giải Câu 41 Bài: Luyện tập sgk Toán 9 tập 2 Trang 83

Câu 41: Trang 83 - SGK Toán 9 tập 2

Qua điểm A nằm bên ngoài đường tròn (O) vẽ hai cát tuyến ABC và AMN sao cho hai đường thẳng BN và CM cắt nhau tại một điểm S nằm bên tròn đường tròn.

Chứng minh: + = $2$ .

Bài làm:

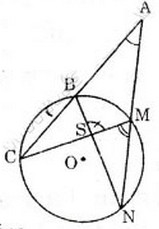
Ta có: là góc có đỉnh nằm ngoài (O) => = $\frac{1}{2}$ . (sđ cung CN - sđ cung BM) (1)

là góc có đỉnh nằm trong (O) => = . (sđ cung CN + sđ cung BM) (2)

Cộng 2 vế (1) và (2) ta có:

+ = . (sđ cung CN - sđ cung BM) + . (sđ cung CN + sđ cung BM)

= . $2$. sđ cung CN = sđ cung CN.

Mặt khác: là góc nội tiếp chắn cung CN của (O) => = . sđ cung CN

=> sđ cung CN = .

=> + = . (đpcm)