Giải câu 5 bài 2: Đồ thị của hàm số y = ax^2 (a ≠ 0) sgk Toán đại 9 tập 2 Trang 37

1 Đánh giá

Câu 5: trang 37 sgk toán lớp 9 tập 2

Cho ba hàm số: $y=\frac{1}{2}x^{2}; y=x^{2}; y=2x^{2}$

a. Vẽ đồ thị của ba hàm số này trên cùng một mặt phẳng tọa độ.

b. Tìm ba điểm A, B, C có cùng hoành độ x = -1,5 theo thứ tự nằm trên ba đồ thị. Xác định tung độ tương ứng của chúng.

c. Tìm ba điểm A'; B'; C' có cùng hoành độ x = 1,5 theo thứ tự nằm trên ba đồ thị. Kiểm tra tính đối xứng của A và A'; B và B'; C và C'.

d. Với mỗi hàm số trên, hãy tìm giá trị của x để hàm số đó có giá trị nhỏ nhất.

Bài làm:

a. Vẽ đồ thị hàm số $y=\frac{1}{2}x^{2}$

Cho $x =\pm 1\Rightarrow y=\frac{1}{2}$

Ta được điểm $M(1; \frac{1}{2});N(-1; \frac{1}{2})$

Vẽ đường cong $(P_{1})$ đi qua gốc tọa độ O và hai điểm M; N vừa xác định, ta được đồ thị hàm số $y=\frac{1}{2}x^{2}$

Vẽ đồ thị hàm số $y=x^{2}$

Cho $x =\pm 1\Rightarrow y=1$

Ta được điểm $P(1;1);Q(-1;1)$

Vẽ đường cong $(P_{2})$ đi qua gốc tọa độ O và hai điểm P; Q vừa xác định, ta được đồ thị hàm số $y=x^{2}$

Vẽ đồ thị hàm số $y=2x^{2}$

Cho $x =\pm 1\Rightarrow y=2$

Ta được điểm $R(1;2);S(-1;2)$

Vẽ đường cong $(P_{3})$ đi qua gốc tọa độ O và hai điểm R; S vừa xác định, ta được đồ thị hàm số $y=2x^{2}$

Ta được đồ thị của ba hàm số:

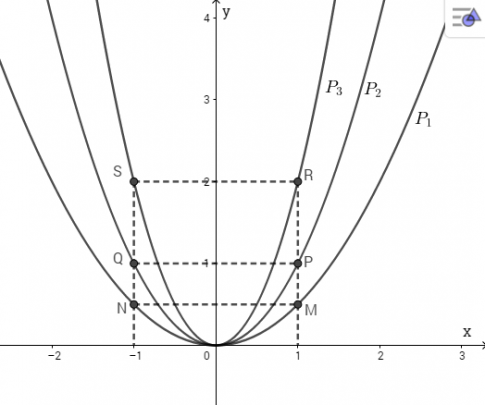
b. Ta có hoành độ $x=-1,5$

Thay giá trị của x vào ba hàm số ta được:

$y=\frac{1}{2}x^{2}\Rightarrow y=\frac{1}{2}.(-1,5)^{2}=1,125$

Vậy điểm $A(-1,5;1,125)$

$y=x^{2}\Rightarrow y=(-1,5)^{2}=2,25$

Vậy điểm $B(-1,5;2,25)$

$y=2x^{2}\Rightarrow y=2.(-1,5)^{2}=4,5$

Vậy điểm $C(-1,5;4,5)$

Ta biểu diễn được các điểm đó trên đồ thị như sau:

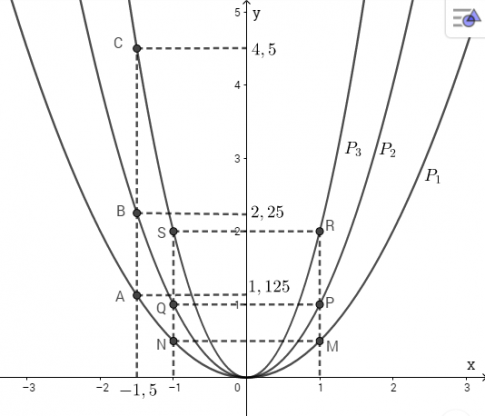
c. Ta có hoành độ $x=1,5$

Thay giá trị của x vào ba hàm số ta được:

$y=\frac{1}{2}x^{2}\Rightarrow y=\frac{1}{2}.1,5^{2}=1,125$

Vậy điểm $A'(1,5;1,125)$

$y=x^{2}\Rightarrow y=1,5^{2}=2,25$

Vậy điểm $B'(1,5;2,25)$

$y=2x^{2}\Rightarrow y=2.1,5^{2}=4,5$

Vậy điểm $C'(1,5;4,5)$

Ta có thể xác định được các điểm A'; B'; C' trên đồ thị hàm số:

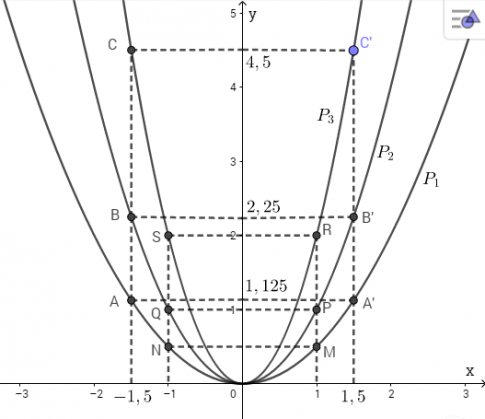
Ta thấy A và A'; B và B'; C và C' đối xứng với nhau qua trục Oy.

d. Trong ba hàm số đã cho, có hệ số a > 0 nên điểm thấp nhất của đồ thị là điểm O(0; 0).

Vậy với $x=0$ thì hàm số có giá trị nhỏ nhất.

53 lượt xem

Cập nhật: 07/09/2021

Xem thêm bài viết khác

Xem thêm Toán 9 tập 2