Giải câu 6 trang 49 toán VNEN 9 tập 1

Câu 6: Trang 49 sách VNEN 9 tập 1

Trên mặt phẳng tọa độ Oxy cho ba điểm A(a; 0); B(0; b) (với a > 0, b > 0) và C(1; 2) như trên hình 12.

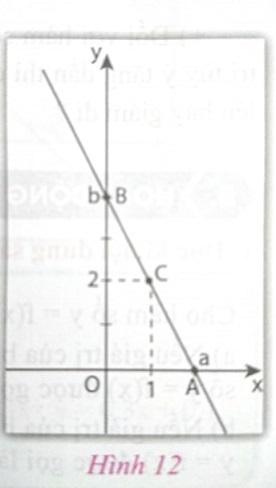
a) Viết phương trình đường thẳng đi qua hai điểm A, B

b) Tìm hệ thức liên hệ giữa a, b sao cho ba điểm A, B, C thẳng hàng.

c) Tìm các giá trị của a, b sai cho bao điểm A, B, C thẳng hàng và diện tích tam giác OAB nhỏ nhất.

Bài làm:

a) Gọi phương trình đường thẳng đi qua hai điểm A, B là (d): y = mx + n

Vì (d) đi qua hai điểm A(a; 0) và B(0; b) nên ta được n = b, m =

Vậy phương trình đường thẳng đi qua hai điểm A, B là (d): y = x + b

b) Phương trình đường thẳng đi qua AB là (d): y = x + b

Để A, B, C thẳng hàng thì điểm C (d)

Ta có: 2 = .1 + b $\iff$ b = $\frac{2a}{a-1}$

c) Theo câu b, để A,B,C thẳng hàng thì b =

Ta có: SOAB = $\frac{1}{2}$.OA.OB = $\frac{1}{2}$ab = $\frac{1}{2}$.a.$\frac{2a}{a-1}$ = $\frac{a^2}{a-1}$

Để diện tích tam giác OAB nhỏ nhất thì phải nhỏ nhất

Xét biểu thức P = = a - 1 + $\frac{1}{a-1}$ + 2 $\ge$ 2.$\sqrt{(a-1).\frac{1}{a-1}}$ + 2 = 4

Suy ra MinSOAB = 4 khi $(a-1{)}^2$ = 1 $\iff$ a = 2 $\Rightarrow$ b = 4

Vậy a = 2, b = 4.