Giải VNEN toán 8 bài 5: Diện tích đa giác - Ứng dụng
Giải bài 5: Diện tích đa giác - Ứng dụng - Sách VNEN toán 8 tập 1 trang 138. Phần dưới sẽ hướng dẫn trả lời và giải đáp các câu hỏi trong bài học. Cách làm chi tiết, dễ hiểu. Hi vọng các em học sinh nắm tốt kiến thức bài học.
B. Hoạt động hình thành kiến thức
- Có thể chia một đa giác thành nhiều tam giác được không? Em hãy quan sát hình 138 để thấy đa giác ABCDE được chia thành các tam giác như thế nào?
- Có thể tạo ra tam giác chứa đa giác MNPQR như thế nào?
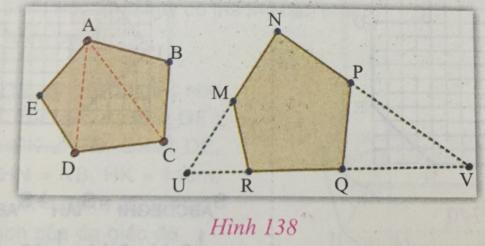
Trả lời:
- Ta có thể chia một đa giác thành nhiều tam giác.
Quan sát hình 138, ta thấy đa giác ABCDE được chia thành 3 hình tam giác bằng cách nối điểm A với D, A với C.
- Ta tạo tam giác chứa đa giác MNPQR như sau:
B1: Kéo dài đoạn thẳng NM cắt đường thẳng kéo dài RQ tại U.
B2: Kéo dài đoạn thẳng NP cắt đường thẳng kéo dài RQ tại V.
Ta được tam giác NUV chứa đa giác MNPQR.
B. BÀI TẬP VÀ HƯỚNG DẪN GIẢI
Kiến thức thú vị
C. Hoạt động luyện tập
Câu 1: Trang 140 toán VNEN 8 tập 1
Trong một khu đất hình chữ nhật người ta đào một ao thả cá, có sơ đồ thiết kế như hình 143, (trên bản vẽ ao thả cá là phần được kẻ sọc).

a) Số liệu trên sơ đồ được tính bằng mét, diện tích của ao thả cá bằng bao nhiêu m![]() ?
?
b) Mật độ thả cá phải phù hợp, nếu thả cá quá dày môi trường nước thiếu ôxi thì cá cũng không lớn được. Tùy vào hình thức nuôi, thả cá trong ao nước tĩnh để tính số con/m![]() mặt nước. Theo kĩ thuật nuôi cá thì: cá chép 2con/10m
mặt nước. Theo kĩ thuật nuôi cá thì: cá chép 2con/10m![]() , trắm đen 1con/15m
, trắm đen 1con/15m![]() . Hỏi ao cá này có thể thả được bao nhiêu con cá trắm đen?
. Hỏi ao cá này có thể thả được bao nhiêu con cá trắm đen?
Câu 2: Trang 141 toán VNEN 8 tập 1
Bạn Giang đã vẽ một hình đa giác như ở hình 144. Biết BC // HK // GF; CF ![]() HK, CK
HK, CK ![]() FE, CK // DE, AH
FE, CK // DE, AH ![]() AB, HN = NB, HK =11cm, HM = 2cm, JK = 3cm, JC = 4cm. Hãy tính diện tích của đa giác đó.
AB, HN = NB, HK =11cm, HM = 2cm, JK = 3cm, JC = 4cm. Hãy tính diện tích của đa giác đó.
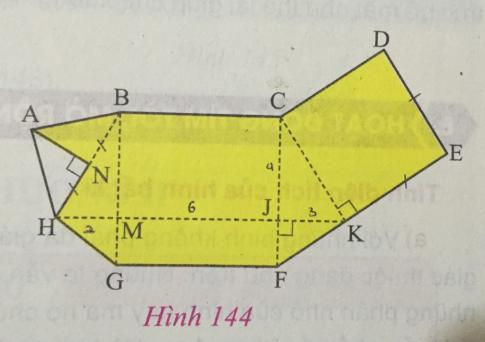
Câu 3: Trang 141 toán VNEN 8 tập 1
Cho hình bình hành ABCD, với diện tích S và AB = a, BC = b. Lấy mỗi cạnh của hình bình hành đó làm cạnh dựng một hình vuông ra phía ngoài hình bình hành. Tính theo a, b và S diện tích của đa giác giới hạn bởi các cạnh của hình vuông mà không là các cạnh của hình bình hành đã cho.
D. Hoạt động vận dụng
Ví dụ 2: Khi thời tiết lạnh, tại sao sinh lực của những động vật rất lớn (có cơ thể lớn) được duy trì dễ hơn so với những động vật nhỏ (có cơ thể nhỏ). Khi thời tiết lạnh , tại sao những động vật nhỏ có máu nóng như chim, chuột luôn cần có sự trao đổi chất cao hơn những động vật lớn như bò, voi.
Ví dụ 3: Con người cần ôxi cho sự thở, để giúp cho sự sống. Phổi của con người thường xốp, được chia thành hàng nghìn túi khí nhỏ (mà không phải là một khối thịt đặc như các khối thịt ở chỗ khác trên cơ thể). Với cấu trúc đó nó giúp cho quá trình hấp thụ ôxi của con người như thế nào?
Ví dụ 4: Hình dạng lùn, mập của cây xương rồng ngày nay có được do sự tiến hóa và thích nghi lâu dài với điều kiện sống khô hạn ở sa mạc. Giải thích tại sao cấu trúc bề mặt như thế lại giúp cho xương rồng thích nghi với đời sống khô hạn ở sa mạc?
Xem thêm bài viết khác
- Giải câu 1 trang 47 toán VNEN 8 tập 1
- Giải VNEN toán 8 bài 5: Hình có tâm đối xứng
- Giải câu 2 trang 145 toán VNEN 8 tập 1
- Giải câu 5 trang 51 toán VNEN 8 tập 1
- Giải VNEN toán 8 bài 7: Phép nhân các phân thức đại số
- Giải câu 3 Trang 43 sách VNEN toán 8 tập 1
- Giải câu 2 trang 113 toán VNEN 8 tập 1
- Giải câu 2 trang 40 sách VNEN toán 8 tập 1
- Giải câu 1 trang 70 toán VNEN 8 tập 1
- Giải câu 1 trang 19 toán VNEN 8 tập 1
- Giải câu 3 trang 54 toán VNEN 8 tập 1
- Giải VNEN toán 8 bài 5: Những hằng đẳng thức đáng nhớ (tiếp)











