Lời giải bài số 38, 41, 50 Đề thi thử THPT quốc gia môn toán năm 2017- Đề tham khảo số 5

Bài làm:

Câu 38: Cho hình chóp S.ABC có tam giác ABC vuông tại A, AB=AC=a, I là trung điểm của BC, hình chiếu vuông góc của S lên mặt phẳng (ABC) là trung điểm của BC, mặt phẳng (SAB) tạo với đáy một góc bằng . Tính khoảng cách từ điểm I đến mặt phẳng (SAB) theo a.

A. .

B. .

C. .

D. .

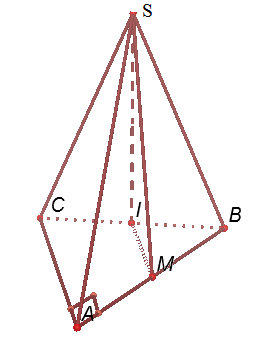Giải: Đáp án A

Gọi M là trung điểm của AB nên

Kẻ . Suy ra $d(I, (SAB))= IH$.

.

.

Câu 41: Cho hình chóp S.ABC có SA=a, SB=b, SC=c và ba cạnh SA, SB, SC đôi một vuông góc. Xác định bán kính của mặt cầu ngoại tiếp hình chóp.

A. .

B. .

C. .

D. .

Giải: Đáp án D

Áp dụng công thức tính nhanh bán kính mặt cầu ngoại tiếp hình chóp trong trường hợp cạnh bên vuông góc với đáy ta có

.

Suy ra .

Câu 50: Trong không gian với hệ tọa độ 0xyz, cho mặt phẳng (P): 2x-y+z+1=0 và hai điểm A(-1,2,-3); B(-9,4,9). Tìm điểm M trên (P) sao cho MA+MB đạt giá trị nhỏ nhất.

A. M(-1,2,-3).

B. M(1,-2,3).

C. M(-1,2,-3).

D. M(-1,2,3).

Giải:

Ta có A, B nằm cùng phía đối với mặt phẳng (P).

Gọi A' là điểm đối xứng của A qua (P), ta có MA'=MA.

Do đó khi M là giao điểm của A'B và (P).

Tìm được A'(3,1,0). Phương trình đường thẳng A'B:

Vậy M(-1,2,3).