Đáp án câu 5 đề 4 kiểm tra học kì 2 toán 7

Câu 5: Cho tam giác ABC vuông tại A, đường cao AH. Trên cạnh BC lấy D sao cho BD= BA.

a. Chứng minh

b. Chứng minh AD là phân giác của

c. Vẽ DK vuông góc với AC (K thuộc AC) chứng minh AK = AH

d. Chứng minh AB+ AC< BC+ 2AH

Bài làm:

Câu 5:

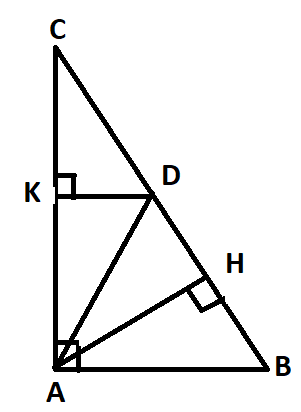
a. Ta có AB= BD (gt)

=> ABD cân tại B => $\widehat{BAD}=\widehat{BDA}$

b. AHD vuông tại H nên $\widehat{HAD}+\widehat{BDA}=90^{\circ}$

Ta lại có mà $\widehat{BAD}=\widehat{BDA}$ (cmt)

=> hay AD là phân giác $\widehat{HAC}$

c. Xét và $\bigtriangleup AHD$ có:

(cmt)

Cạnh AD chung

Do đó => AK= AH

d. Xét theo bất dẳng thức tam giác ta có:

AB< BH + AH

Tương tự ta có:

AC< HC + AH

=> AB+ AC< BH+ HC+ 2AH = BC+ 2AH