Giải câu 1 bài 4: Hai mặt phẳng song song
Câu 1: Trang 71 - SGK hình học 11
Trong mặt phẳng (α) cho hình bình hành ABCD. Qua A, B, C, D lần lượt vẽ bốn đường thẳng a, b, c, d song song với nhau và không nằm trên (α). Trên a, b và c lần lượt lấy ba điểm A’, B’ và C’ tùy ý.
a) Hãy xác định giao điểm D’ của đường thẳng d với mặt phẳng (A’B’C’).
b) Chứng minh A’B’C’D’ là hình bình hành.
Bài làm:
Theo giả thiết ta có hình vẽ sau
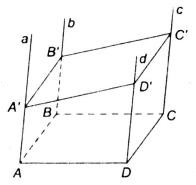
a) Theo giả thiết ta có:
AB // CD (do ABCD là hình bình hành)
và BB' // CC' (do d//c)
=> Mặt phẳng (ABB’A’) // (CDD’C’)
Mặt khác ta có mặt phẳng (A’B’C’) cắt (ABB’A’), cắt (CDD’C’) theo giao tuyến C’D’ // A’B’.
Vậy mặt phẳng (A’B’C’) cắt d tại D’ sao cho C’D’ // A’B’ (1)
b) Chứng minh tương tự câu a, ta có B’C’ // A’D’ (2)
Từ (1) và (2)=>A’B’C’D’ là hình bình hành (đpcm).
Xem thêm bài viết khác
- Giải câu 2 bài 6: Khái niệm về phép dời hình và hai hình bằng nhau
- Giải câu 3 bài 6: Khái niệm về phép dời hình và hai hình bằng nhau
- Giải câu 6 bài 1: Đại cương về đường thẳng và mặt phẳng
- Giải Câu 5 Bài 5: Khoảng cách
- Giải Câu 7 Bài 4: Hai mặt phẳng vuông góc
- Giải Câu 2 Bài 3: Đường thẳng vuông góc với mặt phẳng
- Giải bài 1: Đại cương về đường thẳng và mặt phẳng
- Giải câu 2 bài 7: Phép vị tự
- Giải Câu 1 Bài Vecto trong không gian
- Giải Câu 3 Bài: Bài tập ôn tập chương 3
- Giải Câu 10 Bài 1: Vecto trong không gian
- Giải Câu 2 Bài Ôn tập cuối năm











