Giải câu 11 bài ôn tập chương 4: Bất đẳng thức, bất phương trình sgk Đại số 10 trang 107

Câu 11: trang 107 sgk Đại số 10

a) Bằng cách sử dụng hằng đẳng thức

Hãy xét dấu và \(g(x) = x^2– 2x - {4 \over {{x^2} - 2x}}\)

b) Hãy tìm nghiệm nguyên của bất phương trình sau:

Bài làm:

a) Ta có

Ta lại có ( vì \(a = 1> 0, Δ = 1- 4.3

cùng dấu với \(x^2+x-3\)

Tam thức có hai nghiệm là \(\frac{-1-\sqrt {13}}{2}; \frac{-1+\sqrt {13}}{2}\)

Vậy

• khi \(x < {{ - 1 - \sqrt {13} } \over 2}\)hoặc \(x > {{ - 1 + \sqrt {13} } \over 2}\)
• khi \(\frac{-1-\sqrt {13}}{2} < x < \frac{-1+\sqrt {13}}{2}\)

Ta lại có

cùng dấu với \({{{x^2} - 2x - 2} \over {{x^2} - 2x}}\)

Tam thức có hai nghiệm là \(1-\sqrt 3; 1+\sqrt 3\)

có hai nghiệm là \(x; 2\)

Ta lập bảng xét dấu

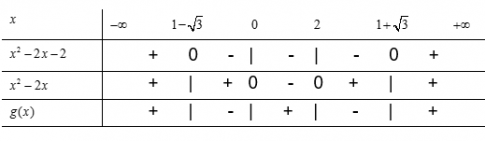
Vậy

• khi \(x \in \left ( -\infty ;1-\sqrt{3} \right )\cup \left ( 0;2 \right )\cup \left ( 1+\sqrt{3}; +\infty \right )\)
• khi \(x \in \left ( 1-\sqrt{3};0 \right )\cup \left ( 2; 1+ \sqrt{3} \right )\)

b)

Ta có

Vậy nghiệm nguyên của bất phương trình là