Giải Câu 17 Bài 3: Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức tam giác sgk Toán 7 tập 2 Trang 63
Câu 17: Trang 63 - SGK Toán 7 tập 2
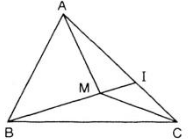
Cho tam giác ABC và M là một điểm nằm trong tam giác. Gọi I là giao điểm của đường thẳng BM và cạnh AC.
a) So sánh MA với MI + IA, từ đó chứng minh MA + MB < IB + IA.
b) So sánh IB với IC + CB, từ đó chứng minh IB + IA < CA + CB.
c) Chứng minh bất đẳng thức MA + MB < CA + CB.
Bài làm:
a) Trong ΔAMI ta có: MA < MI + IA (bất đẳng thức tam giác)
Cộng MB vào hai vế ta được:
MA + MB < MB + MI + IA
Vì MB + MI = IB (do M nằm giữa B và I) nên MA + MB < IB + IA (1) (đpcm)
b) Trong ΔBIC ta có: IB < IC + CB (bất đẳng thức tam giác)
Cộng IA vào hai vế ta được:
IB + IA < IA + IC + CB
Vì IA + IC = CA (do I nằm giữa A và C) nên IB + IA < CA + CB (2) (đpcm)
c) Từ (1) và (2) và theo tính chất bắc cầu ta suy ra:
MA + MB < CA + CB (đpcm)
Xem thêm bài viết khác
- Giải câu 6 bài 2: Giá trị của một biểu thức đại số sgk Toán 7 tập 2 trang 28
- Giải Câu 14 Bài 2: Quan hệ giữa đường vuông góc và đường xiên, đường xiên và hình chiếu sgk Toán 7 tập 2 Trang 60
- Giải câu 19 bài Luyện tập sgk Toán 7 tập 2 trang 36
- Giải bài 3: Đơn thức sgk Toán 7 tập 2 trang 30
- Giải câu 38 bài luyện tập sgk Toán 7 tập 2 trang 41
- Giải câu 4 bài 1: Khái niệm về biểu thức đại số sgk Toán 7 tập 2 trang 27
- Giải câu 22 bài Luyện tập sgk Toán 7 tập 2 trang 36
- Đáp án câu 2 đề 4 kiểm tra học kì 2 toán 7
- Giải Câu 54 Bài 8: Tính chất ba đường trung trực của tam giác sgk Toán 7 tập 2 Trang 80
- Giải bài 4: Số trung bình cộng sgk Toán 7 tập 2 trang 17
- Đáp án câu 3 đề 9 kiểm tra học kì 2 toán 7
- Đáp án câu 1 đề 1 kiểm tra học kì 2 toán 7











