Giải Câu 2 Bài Ôn tập cuối năm

Câu 2: Trang 125 - SGK Hình học 11

Cho tam giác nội tiếp đường tròn tâm \(O\). Gọi \(G\) và \(H\) tương ứng là trọng tâm và trực tâm của tam giác, các điểm \(A',B',C'\) lần lượt là trung điểm của các cạnh \(BC, CA, AB\).

a) Tìm phép vị tự biến \(A, B, C\) tương ứng thành \(A',B',C'\)

b) Chứng minh rằng thẳng hàng.

c) Tìm ảnh của qua phép vị tự \(F\)

d) Gọi lần lượt là trung điểm của các đoạn thẳng \(AH, BH, CH\); \(A_1, B_1, C_1\) theo thứ tự là giao điểm thứ hai của các tia \(AH, BH, CH\) với đường tròn \((O)\); \(A_1',B_1',C_1'\) tương ứng là chân các đường cao đi qua \(A, B, C\). Tìm ảnh của \(A, B, C\), \(A_1, B_1, C_1\) qua phép vị tự tâm \(H\) tỉ số \({1 \over 2}\)

e) Chứng minh chín điểm ,\(A”, B”, C”\),\(A_1',B_1',C_1'\) cùng thuộc một đường tròn (đường tròn này gọi là đường tròn Ơ-le của tam giác \(ABC\))

Bài làm:

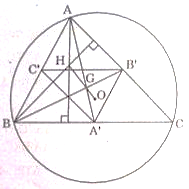
a) Vì là trọng tâm $\Delta ABC$ nên ta có:

\(\eqalign{
& \overrightarrow {GA'} = - {1 \over 2}\overrightarrow {GA} ; \cr
& \overrightarrow {GB'} = - {1 \over 2}\overrightarrow {GB} ; \cr
& \overrightarrow {GC'} = - {1 \over 2}\overrightarrow {GC} \cr}\).

Vậy phép vị tự tâm tỉ số \(k = - {1 \over 2}\) biến \(A, B, C\) thành \(A’, B’, C’\).

b) Vì: là trung điểm của \(BC\) (gt) nên \(OA’ ⊥ BC\) (trong đường tròn (O), đoạn nối tâm với trung điểm dây cung thì vuông góc với dây cung đó)

Ta lại có (định lý Talet trong tam giác ABC)

nên Trong tam giác \(A’B’C’\) thì \(OA’\) là đường cao kẻ từ đỉnh \(A’\).

Tương tự, là đường cao kẻ từ \(B’\), suy ra \(O\) là trực tâm của \(∆A’B’C’\).

Lại có: là trực tâm của \(∆ABC\) và \(O\) là trực tâm của \(∆A’B’C’\), là ảnh của $\Delta ABC$ qua phép vị tự tâm $G$, tỉ số $k=\frac{-1}{2}$

nên là ảnh của \(H\) trong phép vị tự tâm \(G\), tỉ số \(k = - {1 \over 2}\)

=>

Ba điểm \(O, G, H\) thẳng hàng

c) Gọi là ảnh của \(O\) trong phép vị tự \({V_{\left( {G; - {1 \over 2}} \right)}}\) ta có:

\(\eqalign{
& \overrightarrow {GO'} = - {1 \over 2}\overrightarrow {GO} \cr
& \overrightarrow {GO} = - {1 \over 2}\overrightarrow {GH} \to \overrightarrow {OG} = {1 \over 2}\overrightarrow {GH} \cr
& \overrightarrow {OG} + \overrightarrow {GO'} = {1 \over 2}\overrightarrow {GH} - {1 \over 2}\overrightarrow {GO} \cr
& \Rightarrow \overrightarrow {OO'} = {1 \over 2}\left( {\overrightarrow {GH} - \overrightarrow {GO} } \right) \cr
& \Rightarrow \overrightarrow {OO'} = {1 \over 2}\overrightarrow {OH} \cr} \)

Đẳng thức này chứng tỏ điểm là trung điểm của đoạn thẳng \(OH\)

Vậy ảnh của qua phép vị tự tâm , tỉ số \(k = - {1 \over 2}\) là $O'$ trung điểm của $OH$.

d)

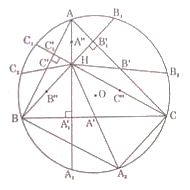
Vì lần lượt là trung điểm của các đoạn thẳng \(AH, BH, CH\)

=>

Vậy là ảnh của các điểm \(A, B, C\) trong phép vị tự \({V_{\left( {H;{1 \over 2}} \right)}}\) (1)

Ta dễ dàng chứng minh được theo thứ tự là trung điểm của các đoạn thẳng \(H{A_1},H{B_1},H{C_1}\) nên:

\(\eqalign{
& \overrightarrow {H{A_1}'} = {1 \over 2}\overrightarrow {H{A_1}} \cr
& \overrightarrow {H{B_1}'} = {1 \over 2}\overrightarrow {H{B_1}} \cr
& \overrightarrow {H{C_1}'} = {1 \over 2}\overrightarrow {H{C_1}} \cr} \)

Như vậy theo thứ tự là ảnh của các điểm \(A_1, B_1, C_1\) trong phép vị tự (2)

Từ (1) (2), ảnh của , \(A_1, B_1, C_1\) qua phép vị tự tâm \(H\) tỉ số \({1 \over 2}\) lần lượt là \(A”, B”, C”\),\(A_1',B_1',C_1'\)

e) Gọi theo thứ tự là các điểm xuyên tâm đối của các điểm \(A, B, C\) qua tâm \(O\) của đường tròn.

Ta chứng minh được tứ giác là hình bình hành, do đó \(H\) và \(A_2\) đối xứng qua \(A’\), ta có:

\(\eqalign{
& \overrightarrow {HA'} = {1 \over 2}\overrightarrow {H{A_2}} \cr
& \overrightarrow {HB'} = {1 \over 2}\overrightarrow {H{B_2}} \cr
& \overrightarrow {HC'} = {1 \over 2}\overrightarrow {H{C_2}} \cr} \)

Như vậy, các điểm theo thứ tự là ảnh của các điểm \(A_2, B_2, C_2\) trong phép vị tự (3)

Từ (1), (2), (3) ta có:

Chín điểm , \(A_1',B_1',C_1'\) theo thứ tự là ảnh của các điểm \(A,B,C,{A_1},{B_1},{C_1},{A_2},{B_2},{C_2}\) trong phép tự vị \({V_{\left( {H;{1 \over 2}} \right)}}\)

mà chín điểm nằm trên đường tròn \((O)\) nên chín điểm nằm trên đường tròn ảnh của đường tròn \((O)\) trong phép vị tự \({V_{\left( {H;{1 \over 2}} \right)}}\)