Giải câu 2 trang 64 sách toán VNEN lớp 7 tập 2

Câu 2: Trang 64 sách toán VNEN 7 tập 2

a) - So sánh các góc của tam giác GLO, biết GL = 6cm, LO = 8cm và OG = 10cm.

- So sánh các cạnh của tam giác UVW biết = 50^o ; = 40^o

b) Hình 13, có AB = AD, ba điể, A, D, C thẳng hàng, điểm E thuộc cạnh AB và DE // BC

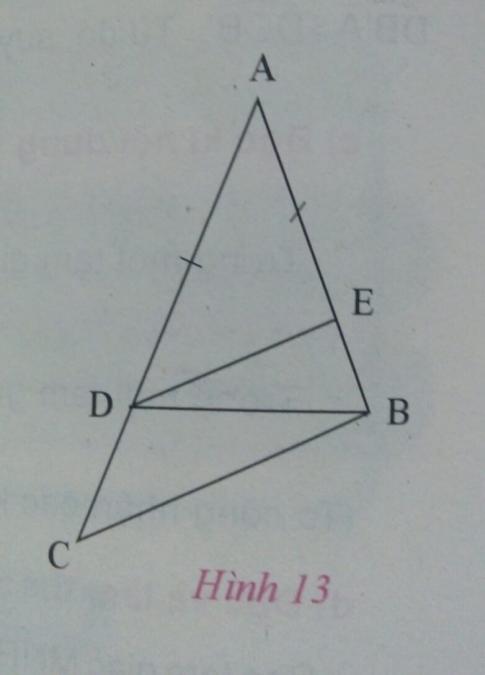
- So sánh hai góc và $\widehat{ACB}$.

- So sánh hai góc và $\widehat{AED}$.

- So sánh hai cạnh AD và AE.

c) - Tam giác ABC có AB = AC và = 60^o . So sánh ba cạnh của tam giác ABC.

- Tam giác LGR có = $\widehat{R}$ = 60^o. So sánh ba cạnh của tam giác LGR.

- Tam giác PQS có = 90^o và = 45^o. So sánh ba cạnh của tam giác PQS.

Bài làm:

a) - Trong tam giác GLO: + Đối diện với cạnh lớn nhất (OG = 10cm) là góc

+ Đối diện với cạnh lớn thứ 2 (LO = 8cm) là góc

+ Đối diện với cạnh nhỏ nhất (GL = 6cm) là góc

Suy ra: > $\widehat{G}$ > $\widehat{O}$

- Trong tam giác UVW biết = 50^o ; = 40^o. Suy ra góc = 90^o

+ Đối diện với góc lớn nhất ( = 90^o) là cạnh UV

+ Đối diện với góc lớn thứ 2 ( = 50^o) là cạnh VW

+ Đối diện với góc nhỏ nhất ( = 40^o) là cạnh UW

Suy ra: UV > VW > UW

b) - Theo giả thiết ta có: AB = AD mà AC = AD + DC => AC = AB + DC > AB

Trong tam giác ABC, do AC > AB => > $\widehat{ACB}$ (góc đối diện tương ứng với 2 cạnh AC và AB)

- Theo giả thiết DE // BC => = $\widehat{ACB}$ (cặp góc đồng vị). Và: $\widehat{ABC}$ = $\widehat{AED}$ (đồng vị) (1)

Theo câu a) thì > $\widehat{ACB}$ (2)

Từ (1) và (2) suy ra: > $\widehat{ADE}$.

- Trong tam giác ADE, có > $\widehat{ADE}$ (chứng minh trên) => AD > AE (cạnh đối diện tương ứng)

c) - Tam giác ABC có AB = AC => tam giác ABC cân tại A => = $\widehat{C}$ (1)

Lại có: = 60^o (2)

Từ (1) và (2) suy ra tam giác ABC là tam giác đều. Vậy AB = AC = BC.

- Tam giác LGR có = $\widehat{R}$ = 60^o. => = 60^o(tổng số đo ba góc trong 1 tam giác bằng 180 độ)

Suy ra tam giác LGR là tam giác đều nên ba cạnh đều bằng nhau.

- Tam giác PQS có = 90^o và = 45^o => = 45^o.

Suy ra QS > PQ = PS (cạnh đối diện lần lượt với 3 góc P, S và Q)