Giải Câu 20 Bài 3: Quan hệ giữa ba cạnh của một tam giác. Bất đẳng thức tam giác sgk Toán 7 tập 2 Trang 64

Câu 20: Trang 64 - SGK Toán 7 tập 2

Một cách chứng minh khác của bất đẳng thức tam giác:

Cho tam giác ABC. Giả sử BC là cạnh lớn nhất. Kẻ đường vuông góc AH đến đường thẳng BC (H thuộc BC).

a) Dùng nhận xét về cạnh lớn nhất trong tam giác vuông ở Bài 1 để chứng minh AB + AC > BC.

b) Từ giả thiết về cạnh BC, hãy suy ra hai bất đẳng thức tam giác còn lại.

Bài làm:

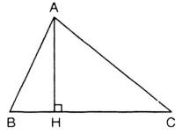
a)

Trong ΔAHC vuông tại H ta có: HC < AC (quan hệ giữa đường xiên và hình chiếu)

Trong ΔAHB vuông tại H ta có: HB < AB (quan hệ giữa đường xiên và hình chiếu)

Cộng vế theo vế hai bất đẳng thức ta có:

HB + HC < AC + AB

Vì HB + HC = BC (do H nằm giữa B và C) nên BC < AC + AB (1)

b) Tam giác ABC có BC là cạnh lớn nhất (gt)

nên suy ra AB < BC và AC < BC.

Vì AB, AC > 0, ta cộng thêm AC (hoặc AB) vào vế phải của bất đẳng thức

nên AB < BC + AC; AC < BC + AB (đpcm)