Giải câu 3 bài 3: Một số phương trình lượng giác thường gặp

Câu 3: Trang 37 - sgk đại số và giải tích 11

Giải các phương trình sau :

a)

b)

c)

d)

Bài làm:

a) (1)

Đặt t = cos(x/2), t ∈ [-1 ; 1]

(1) <=> (1 - t²) - 2t + 2 = 0 ⇔ t² + 2t -3 = 0 ⇔ t = 1 hoặc t = -3 (loại vì không t/m điều kiện)

Với t = 1 ⇔ cos(x/20 = 1 ⇔ x/2 = k2π ⇔ x = 4kπ, k ∈ Z.

b) (2)

Đặt t = sinx, t ∈ [-1 ; 1]

(2) ⇔ 8(1 - t²) + 2t - 7 = 0 ⇔ 8t² - 2t - 1 = 0 ⇔ t = hoặc t = $-\frac{1}{4}$

Với t =

Với t =

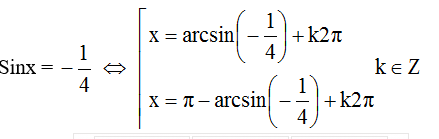
c) (3)

Đặt t = tanx với t ∈ R

(3) ⇔ 2t² + 3t + 1 = 0 ⇔ t = -1 hoặc t =

Với t = -1

tan x = 1 =>

Với t =

tan x = => $x = arctan(\frac{-1}{2}) + k\pi , k\epsilon Z$

d) (4)

Đặt t = tanx với t ∈ R

(4) ⇔ t - (2/t) + 1 = 0 ⇔ t² + t - 2 = 0 ⇔ t = 1 hoặc t = -2.

Với t = 1

tan x = 1 =>

Với t = -2

tan x = - 2 =>