Giải câu 3 trang 125 toán VNEN 9 tập 1
Câu 3: Trang 125 sách VNEN 9 tập 1
Cho đường tròn tâm O đường kính AB. Gọi I là trung điểm của AO. Vẽ đường tròn tâm I đường kính AO.
a) Chứng minh đường tròn (O) và (I) tiếp xúc với nhau tại A.
b) Qua A vẽ đường thẳng cắt (O) tại C và cắt (I) tại D (C, D khác A). Chứng minh ID // OC và OD // CB.
c) Lấy K trên đoạn CB sao cho BK = 2KC. Chứng minh AK đi qua trung điểm của OC.
Bài làm:
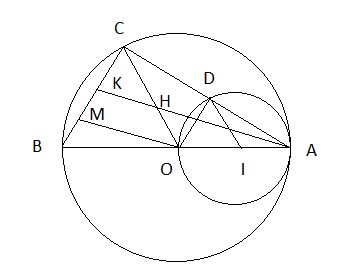
a) Vì I là trung điểm của OA nên OI = OA - IA nên hai đường tròn tiếp xúc trong tại A.
b) * ![]() IAD có IA = ID nên
IAD có IA = ID nên ![]() IAD cân tại I$\Rightarrow $ $\widehat{IAD}$ = $\widehat{IDA}$
IAD cân tại I$\Rightarrow $ $\widehat{IAD}$ = $\widehat{IDA}$
![]() OAC có OA = OC nên
OAC có OA = OC nên ![]() OAC cân tại O $\Rightarrow $ $\widehat{OAC}$ = $\widehat{OCA}$
OAC cân tại O $\Rightarrow $ $\widehat{OAC}$ = $\widehat{OCA}$
Mặt khác: ![]() = $\widehat{OAC}$ $\Rightarrow $ $\widehat{IDA}$ = $\widehat{OCA}$ hay ID // OC
= $\widehat{OAC}$ $\Rightarrow $ $\widehat{IDA}$ = $\widehat{OCA}$ hay ID // OC
* Ta chứng minh được ID // OC, theo định lý Ta-lét trong ![]() OAC có:
OAC có:
![]() = $\frac{IA}{OA}$ = $\frac{2IA}{2OA}$ = $\frac{OA}{BA}$ hay OD // CB.
= $\frac{IA}{OA}$ = $\frac{2IA}{2OA}$ = $\frac{OA}{BA}$ hay OD // CB.
c) Gọi M là trung điểm BK
Tam giác ABK có: M là trung điểm BK, O là trung điểm AB nên OM là đường trung bình ![]() ABK
ABK
![]() MO // KA hay MO // KH
MO // KA hay MO // KH
Tam giác OBC có MO // KH, K là trung điểm CM nên MO là đường trung bình ![]() OBC
OBC
![]() H là trung điểm CO
H là trung điểm CO
Vậy AK đi qua trung điểm CO (đpcm).
Xem thêm bài viết khác
- Giải câu 1 trang 96 toán VNEN 9 tập 1
- Giải câu 3 trang 72 toán VNEN 9 tập 1
- Giải câu 4 trang 15 toán VNEN 9 tập 1
- Giải toán VNEN 9 bài 4: Tính chất đồng biến, nghịch biến của hàm số y = ax + b
- Giải câu 8 trang 34 toán VNEN 9 tập 1
- Giải câu 1 trang 93 toán VNEN 9 tập 1
- Giải câu 4 trang 61 toán VNEN 9 tập 1
- Giải câu 4 trang 85 toán VNEN 9 tập 1
- Giải câu 2 trang 13 sách toán VNEN lớp 9 tập 1
- Giải câu 3 trang 52 toán VNEN 9 tập 1
- Giải toán VNEN 9 bài 2: Quan hệ giữa đường kính và dây cung của đường tròn
- Giải câu 3 trang 111 toán VNEN 9 tập 1











