Giải câu 4 bài: Khối đa diện lồi và khối đa diện đều

Bài 4:Trang 18 - sgk hình học 12

Cho hình bát diện đều ABCDEF(h.1.24). Chứng minh rằng

a) Các đoạn thẳng AF, BD, CE đôi một vuông góc với nhau và cắt nhau tại trung điểm mỗi đường.

b) ABFD, AEFC và BCDE là những hình vuông.

Bài làm:

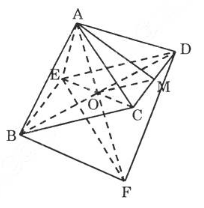a) Ta có EA=EF, CA=CF và BA=BF, DA=DF nên bốn điểm B, C, D, E cùng nằm trong mặt phẳng trung trực của EF.

Trong mặt phẳng đó BE=ED=DC=CB nên BEDC là hình thoi nên hai đường chéo BD, EC giao nhau tại trung điểm mỗi đường.

Tương tự, ta chứng minh được AF và BD cũng giao nhau tại O.

Tứ giác ABDF là hình thoi nên .

Tương tự, ta chứng minh được và $BD\perp EC$.

b) Ta có và $AF\perp EC$ suy ra $AF\perp (BEDC)\Rightarrow AF\perp CD$.

Gọi M là trung điểm của CD. Vì tam giác ACD cân tại A nên .

Vì vậy . (1)

Xét tam giác BCD có O là trung điểm của BD, M là trung điểm của CD nên OM là đường trung bình của tam giác BCD (2).

Từ (1) và (2) suy ra BECD là hình vuông.

Chứng minh tương tự AEFC và ABFD là hình vuông.