Giải câu 4 bài: Khái niệm về khối đa diện
Bài 4 :Trang 12-sgk hình học12
Chia một khối lập phương thành sáu khối tứ diện bằng nhau.
Bài làm:
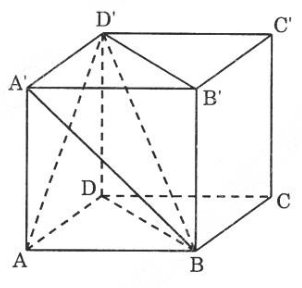 Trước hết, ta chia khối lập phương thành hai khối lăng trụ bằng nhau ABD.A'B'D' và BCD.B'C'D' vì chúng đối xứng qua mặt phẳng (BDD'B').
Trước hết, ta chia khối lập phương thành hai khối lăng trụ bằng nhau ABD.A'B'D' và BCD.B'C'D' vì chúng đối xứng qua mặt phẳng (BDD'B').
Trong lăng trụ ABD.A'B'D' ta xét ba khối lăng trụ D'A'AB, D'A'B'B, D'ABD ta có: D'A'AB và D'A'B'B bằng nhau vì đối xứng qua mặt phẳng (A'D'C'B).
D'S'AB và D'ADB bằng nhau vì đối xứng qua (ABC'D').
Tương tự, ta cũng chia hình lăng trụ BCD.B'C'D' thành 3 khối tứ diện D'B'BC, D'B'C'C, D'BDC. Các khối tứ diện này bằng nhau và bằng ba khối tứ diện trên.
Xem thêm bài viết khác
- Giải câu 2 bài: Mặt cầu
- Dạng 1: Tìm toạ độ của một vectơ và các yếu tố liên quan đến vectơ thoả mãn một số điều kiện cho trước
- Dạng 4: Khối chóp có một mặt bên vuông góc với đáy
- Giải câu 7 bài: Ôn tập chương I: Khối đa diện
- Giải bài 2: Mặt cầu
- Giải câu 4 bài: Hệ tọa độ trong không gian
- Giải câu 6 bài: Hệ tọa độ trong không gian
- Giải câu 5 bài: Ôn tập chương I: Khối đa diện
- Giải câu 37 bài: Ôn tập chương II
- Giải câu 9 bài: Ôn tập chương III
- Giải câu 5 bài: Phương trình đường thẳng trong không gian
- Dạng 2: Viết phương trình đường thẳng d là giao tuyến của hai mặt phẳng Toán 12











