Giải câu 2 bài: Khối đa diện lồi và khối đa diện đều
Bài 2: Trang 18 -sgk hình học 12
Cho hình lập phương (H). Gọi (H') là hình bát diện đều có các đỉnh là tâm của các mặt của (H). Tính tỉ số diện tích toàn phần của (H) và (H').
Bài làm:
 Gọi
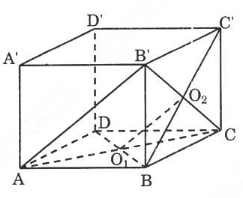
Gọi ![]() lần lượt là tâm của hai mặt ABCD và BCC'B' và a là cạnh của hình lập phương.
lần lượt là tâm của hai mặt ABCD và BCC'B' và a là cạnh của hình lập phương.
Dễ thấy ![]() là đường trung bình của tam giác AB'C nên $O_{1}O_{2} \parallel AB'$ và $O_{1}O_{2}=\frac{1}{2} AB'=\frac{a \sqrt{2}}{2}$.
là đường trung bình của tam giác AB'C nên $O_{1}O_{2} \parallel AB'$ và $O_{1}O_{2}=\frac{1}{2} AB'=\frac{a \sqrt{2}}{2}$.
Chứng minh tương tự cho các khoảng cách các tâm còn lại và suy ra rằng tâm của các mặt của (H) là một khối đa diện 8 mặt là các tam giác đều có cạnh là ![]() .
.
Diện tích toàn phần của hình lập phương là ![]() .
.
Diện tích một mặt của hình bát diện đều cạnh bằng ![]() là $S=(\frac{a\sqrt{2}}{2})^{2}.\frac{\sqrt{3}}{4}=\frac{a^{2}\sqrt{3}}{8}$
là $S=(\frac{a\sqrt{2}}{2})^{2}.\frac{\sqrt{3}}{4}=\frac{a^{2}\sqrt{3}}{8}$
Diện tích toàn phần của hình bát diện đều là ![]() .
.
Vậy ![]()
Xem thêm bài viết khác
- Giải câu 4 bài: Ôn tập chương I: Khối đa diện
- Giải câu 9 bài: Phương trình đường thẳng trong không gian
- Dạng 3: Khối lăng trụ xiên
- Dạng 2: Chứng minh các hệ thức vectơ
- Giải câu 1 bài: Hệ tọa độ trong không gian
- Giải câu 2 bài: Khái niệm về khối đa diện
- Giải câu 1 bài: Khái niệm về mặt tròn xoay
- Giải câu 3 bài: Phương trình mặt phẳng
- Giải bài: Ôn tập chương I: Khối đa diện
- Giải bài 2: Phương trình mặt phẳng
- Giải câu 3 bài: Khái niệm về thể tích của khối đa diện
- Giải câu 1 bài: Phương trình đường thẳng trong không gian











