Giải câu 10 bài: Ôn tập chương I: Khối đa diện

Bài 10: Trang 26 - sgk hình học 12

Cho hình lăng trụ đứng tam giác ABC.A'B'C' có tất cả các cạnh đều bằng a.

a) Tính thể tích khối tứ diện A'BB'C.

b) Mặt phẳng đi qua A'B' và trọng tâm tam giác ABC, cắt AC và BC lần lượt tại E và F. Tính thể tích khối chóp C.A'B'FE.

Bài làm:

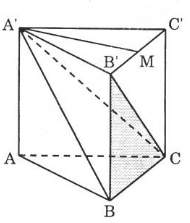a) Gọi M là trung điểm của B'C'.

Do tam giác A'B'C' là tam giác đều nên , hơn nữa ABC.A'B'C' là hình lăng trụ đứng nên $(A'B'C') \perp (BCC'B')$ suy ra $A'M \perp (BB'C'C)$.

Ta có , $S_{BB'C}=\frac{1}{2}BB'.BC=\frac{1}{2}a^{2}$.

.

b) Gọi G là trọng tâm của tam giác ABC.

Xét (GA'B') và (ABC) có

và $A'B' \parallel AB$ nên giao tuyến của hai mặt phẳng là đường thẳng đi qua G và song song với AB lần lượt cắt AC và AB tại E và F.

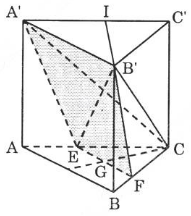Hơn nữa .

Ta có

Gọi K là trung điểm của AB.

Hơn nữa .

Vậy

Cách 2: Thể tích hình chóp bằng tổng thể tích hai hình chóp

• là thể tích hình chóp đỉnh B' đáy là tam giác CEF.
• là thể tích hình chóp đỉnh B', đáy là tam giác A'EC.