Dạng 4: Khối chóp có một mặt bên vuông góc với đáy
Dạng 4: Khối chóp có một mặt bên vuông góc với đáy
Bài làm:
I.Phương pháp giải
Trên mặt bên thuộc mặt phẳng vuông góc với đáy, ta dựng đoạn thẳng SH vuông góc với cạnh đáy của hình chóp. Đoạn thẳng đó cũng là đường cao của khối chóp. Từ đó ta tính diện tích mặt đáy và tính được thể tích khối chóp.
II.Bài tập vận dụng
Bài tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt bên SAB là tam giác đều nằm trong mặt phẳng vuông góc với đáy ABCD. Tính thể tích khối chóp.
Bài giải:

Ta kẻ SH vuông góc với AB. Do tam giác SAB đều nên H là trung điểm của AB ![]()
Mà ![]() nên SH là đường cao của hình chóp S.ABCD.
nên SH là đường cao của hình chóp S.ABCD.
Vậy ta có:
![]() .
.
Bài tập 2: Cho tứ diện ABCD có ABC là tam giác đều, BCD là tam giác vuông cân tại D, ![]() và AD hợp với (BCD) một góc $60^{\circ}$. Tính thể tích tứ diện ABCD.
và AD hợp với (BCD) một góc $60^{\circ}$. Tính thể tích tứ diện ABCD.
Bài giải:
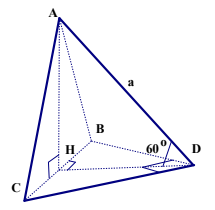
Gọi cạnh của tam giác đều ABC là a.
Ta kẻ AH vuông góc với BC. Do tam giác ABC đều nên H là trung điểm của BC ![]() .
.
Có ![]() mà $AH \perp BC$ nên $AH \perp (BCD)$. Do đó AH là đường cao của hình chóp.
mà $AH \perp BC$ nên $AH \perp (BCD)$. Do đó AH là đường cao của hình chóp.
Có ![]() , AD hợp với (BCD) một góc $60^{\circ}$ suy ra $\widehat{ADH}=60^{\circ}$.
, AD hợp với (BCD) một góc $60^{\circ}$ suy ra $\widehat{ADH}=60^{\circ}$.
Tam giác ADH vuông tại H có:![]() và $HD=AD.cot60^{\circ}=\frac{a\sqrt{3}}{3}$.
và $HD=AD.cot60^{\circ}=\frac{a\sqrt{3}}{3}$.
BCD là tam giác vuông cân tại D, H là trung điểm của BC nên BC = 2HD = ![]() .
.
Vậy![]() .
.
Xem thêm bài viết khác
- Giải câu 37 bài: Ôn tập chương II
- Giải câu 9 bài: Mặt cầu
- Giải câu 2 bài: Mặt cầu
- Giải câu 12 bài: Ôn tập chương I: Khối đa diện
- Giải câu 1 bài: Khái niệm về mặt tròn xoay
- Giải câu 1 bài: Khái niệm về khối đa diện
- Giải câu 10 bài: Phương trình đường thẳng trong không gian
- Giải bài 2: Khối đa diện lồi và khối đa diện đều
- Dạng 3: Khối lăng trụ xiên
- Giải câu 8 bài: Mặt cầu
- Giải câu 2 bài: Khối đa diện lồi và khối đa diện đều
- Giải câu 8 bài: Khái niệm về mặt tròn xoay











