Giải câu 6 bài: Ôn tập chương I: Khối đa diện

1 Đánh giá

Bài 6: Trang 26 - sgk hình học 12

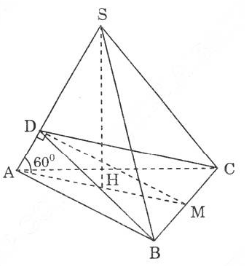
Cho hình chóp tam giác đều S.ABC có cạnh AB bằng a. Các cạnh bên SA, SB, SC tạo với đáy một góc bằng $60^{0}$ . Gọi D là giao điểm của SA với mặt phẳng qua BC và vuông góc với SA.

a) Tính tỉ số thể tích của hai khối chóp S.DBC và S.ABC.

b) Tính thể tích khối chóp S.DBC.

Bài làm:

Hướng dẫn vẽ hình

Bước 1: Vẽ hình chóp đều SABC , lưu ý vẽ đáy là tam giác trước, xác định tâm và từ điểm đó dựng đường thẳng vuông góc với (ABC) sau đó lấy điểm S.
Bước 2: Vẽ mặt phẳng qua BC vuông góc với SA bằng cách dựng $BD \perp SA \Rightarrow CD \perp SA$

Giải:

a) Vì hình chóp S.ABC là hình chóp đều nên chân đường cao H là tâm của đường tròn ngoại tiếp đáy hay $SH \perp (ABC)$ .

$\Rightarrow \widehat{(SA, (ABC))}=\widehat{(SA,AH)}=\widehat{SAH}=60^{0}$ .

Gọi M là trung điểm của BC thì AM là đường cao của tam giác đều ABC.

$AM=\frac{a \sqrt{3}}{2} \Rightarrow AH=\frac{2}{3}AM=\frac{a\sqrt{3}}{3}$ .

$\Rightarrow SA=\frac{AH}{\cos 60^{0}}=\frac{2a\sqrt{3}}{3}$ .

Do $(DBC) \perp SA \Rightarrow DM \perp SA \Rightarrow AD=AM.\cos 60^{0}=\frac{a \sqrt{3}}{4}$

$\Rightarrow SD=SA-AD=\frac{5a\sqrt{3}}{12}$

Áp dụng công thức tỉ số thể tích ta được

$\frac{V_{S.DBC}}{V_{S.ABC}}=\frac{SD}{SA}.\frac{SB}{SB}.\frac{SC}{SC}=\frac{5a \sqrt{3}}{12}: \frac{2a \sqrt{3}}{3}=\frac{5}{8}$ .

b) Ta có $S_{ABC}=\frac{a^{2}\sqrt{3}}{4}, SH=AH. \tan 60^{0}=a$

$\Rightarrow V_{SABC}=\frac{1}{3}.SH.S_{ABC}=\frac{a^{3}\sqrt{3}}{12}$ .

$\Rightarrow V_{S.DBC}=\frac{5}{8}V_{S.ABC}=\frac{5a^{3}\sqrt{3}}{96}$

1 lượt xem

Cập nhật: 07/09/2021

Xem thêm bài viết khác

Xem thêm Hình học 12