Giải câu 9 bài: Ôn tập chương I: Khối đa diện

1 Đánh giá

Bài 9: Trang 26 - sgk hình học 12

Cho hình chóp tứ giác đều S.ABCD có đáy là hình vuông cạnh a, cạnh bên tạo với đáy một góc $60^{0}$ . Gọi M là trung điểm của SC. Mặt phẳng đi qua AM và song song với BD, cắt SB tại E và cắt SD tại F. Tính thể tích khối chóp S.AEMF

Bài làm:

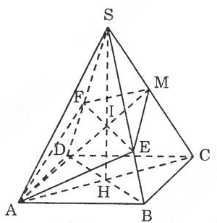Giải: Gọi giao của AC và BD là H, giao của AM và SH là I. Ta có $SH \perp (ABCD)$ .

Xét mặt phẳng (P) và (SBD) có I là giao điểm của (P) và (SBD), $BD \parallel (P)$ nên giao tuyến của (P) và (SBD) là đường thẳng đi qua I và song song với BD lần lượt cắt SB và SD tại E và F.

Ta có $\widehat{(SA, (ABCD))}=\widehat{(SA, AH)}=\widehat{SAH}=60^{0}$ .

Xét tam giác SAC có $SH=AH. \tan 60^{0}=\frac{1}{2}AC. \sqrt{3}=\frac{a \sqrt{6}}{2}$

Hơn nữa ta có I là trọng tâm của tam giác SAC nên $\frac{SI}{SH}=\frac{2}{3}=\frac{SF}{SD}.\frac{SE}{SB}$ .

Suy ra $\frac{V_{SFAE}}{V_{SDAB}}=\frac{SF}{SD}.\frac{SA}{SA}.\frac{SE}{SB}=\frac{2}{3}.\frac{2}{3}=\frac{4}{9}$

$\frac{V_{SFME}}{V_{SDCB}}=\frac{SF}{SD}.\frac{SM}{SC}.\frac{SE}{SB}=\frac{2}{3}.\frac{1}{2}.\frac{2}{3}=\frac{2}{9}$ .

Mặt khác $V_{SABD}=V_{SDCB}=\frac{1}{2}V_{SABCD}=\frac{1}{2}.\frac{1}{3}.SH.S_{ABCD}=\frac{a^{3}\sqrt{6}}{12}$

Vậy $V_{S.AEMF}=V_{SFAE}+V_{SFME}=\frac{a^{3}\sqrt{6}}{18}$ .

2 lượt xem

Cập nhật: 07/09/2021

Xem thêm bài viết khác

Xem thêm Hình học 12