Giải câu 5 bài: Ôn tập chương I: Khối đa diện

Bài 5: Trang 26 - sgk hình học 12

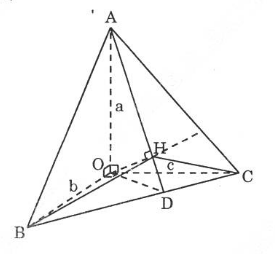
Cho hình chóp O.ABC có ba cạnh OA, OB, OC đôi một vuông góc với nhau và OA=a, OB=b, OC=c. Hãy tính đường cao OH của hình chóp.

Bài làm:

Kẻ $OH \perp (ABC) \Rightarrow OH \perp BC$ .

Hơn nữa $\left.\begin{matrix} OA \perp OB\\ OA \perp OC\end{matrix}\right\} \Rightarrow OA \perp BC$

$\Rightarrow BC \perp (AOH)$ .

Kéo dài AH cắt BC tại D nên $BC \perp AD$ . Suy ra H nằm trên đường cao AD.

Chứng minh tương tự ta được H là trực tâm của tam giác ABC.

Xét tam giác AOD có $\widehat{AOD}=90^{0}$ (do $A O ⊥ (O C B) \Rightarrow A O ⊥ O D$ ) và $O H ⊥ A D$ (do $O H ⊥ (A B C))$

$\frac{1}{OH^{2}}=\frac{1}{OA^{2}}+\frac{1}{OD^{2}}$ . (1)

Xét tam giác OBC vuông tại O có $OD \perp BC$ (do $B C ⊥ (A O H)$ )

$\frac{1}{OD^{2}}=\frac{1}{OB^{2}}+\frac{1}{OC^{2}}$ (2)

Từ (1) và (2) suy ra $\frac{1}{OH^{2}}=\frac{1}{OA^{2}}+\frac{1}{OB^{2}}+\frac{1}{OC^{2}}=\frac{1}{a^{2}}+\frac{1}{b^{2}}+\frac{1}{c^{2}}$

$\Rightarrow OH=\frac{abc}{\sqrt{a^{2}.b^{2}+b^{2}.c^{2}+c^{2}.a^{2}}}$ .

Cập nhật: 07/09/2021

Xem thêm bài viết khác

Nhiều người quan tâm