Dạng 2: Chứng minh các hệ thức vectơ

Dạng 2: Chứng minh các hệ thức vectơ

Bài làm:

Sử dụng quy tắc ba điểm đối với phép cộng, phép trừ và các tính chất của các phép toán về vectơ để biến đổi các hệ thức vectơ.

Bài tập 1: Cho tứ diện ABCD. Gọi E và F lần lượt là trung điểm của AB và CD, I là trung điểm của EF.

Bài giải:

a) Chứng minh rằng:

$\vec{IA}+\vec{IB}+\vec{IC}+\vec{ID}=0$ .

b) Với điểm M bất kì trong không gian, hãy chứng minh rằng:

$4\vec{MI}=\vec{MA}+\vec{MB}+\vec{MC}+\vec{MD}$ .

Bài giải:

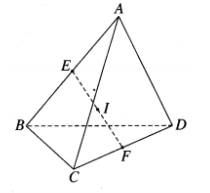
a) Ta có:

$\vec{IA}+\vec{IB}=2\vec{IE}$

$\vec{IC}+\vec{ID}=2\vec{IF}$

$\Rightarrow \vec{IA}+\vec{IB}+\vec{IC}+\vec{ID}=2(\vec{IE}+\vec{IF})$

Vì I là trung điểm của EF nên $\vec{IE}+\vec{IF}=0\Rightarrow \vec{IA}+\vec{IB}+\vec{IC}+\vec{ID}=0$ . (đpcm)

b) Ta có:

$\vec{MI}=\vec{MA}+\vec{AI}$

$\vec{MI}=\vec{MB}+\vec{BI}$

$\vec{MI}=\vec{MC}+\vec{CI}$

$\vec{MI}=\vec{MD}+\vec{DI}$

$\Rightarrow 4\vec{MI}=\vec{MA}+\vec{MB}+\vec{MC}+\vec{MD}+\vec{AI}+\vec{BI}+\vec{CI}+\vec{DI}$

Mà theo câu a) ta có $\vec{IA}+\vec{IB}+\vec{IC}+\vec{ID}=0 \Rightarrow 4\vec{MI}=\vec{MA}+\vec{MB}+\vec{MC}+\vec{MD}$ .

Bài tập 2: Cho tứ diện ABCD. Chứng minh rằng $\overrightarrow{AC}$ + $\overrightarrow{BD}$ = $\overrightarrow{AD}$ + $\overrightarrow{BC}$ .

Bài giải:

Ta có:

$\vec{AC}=\vec{AD}+\vec{DC}$

$\vec{BD}=\vec{BC}+\vec{CD}$

$\Rightarrow \vec{AC}+\vec{BD}=\vec{AD}+\vec{DC}+\vec{BC}+\vec{CD}$

Mà $\vec{DC}+\vec{CD}=0$ nên $\vec{AC}+\vec{BD}=\vec{AD}+\vec{BC}$

Cập nhật: 07/09/2021

Xem thêm bài viết khác