Giải câu 6 bài: Khái niệm về thể tích của khối đa diện
Bài 6: Trang 26 - sgk hình học 12
Cho hai đường chéo nhau d và d'. Đoạn thẳng AB có độ dài a trượt trên d, đoạn thẳng CD có độ dài b trượt trên d'. Chứng minh rằng khối tứ diện ABCD có thể tích không đổi.
Bài làm:
Qua A ta dựng đường thẳng ![]() .
.
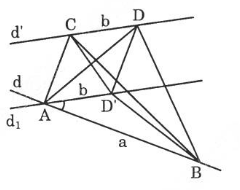 Gọi (P) là mặt phẳng xác định bởi
Gọi (P) là mặt phẳng xác định bởi ![]() và d thì $d' \parallel (P) \Rightarrow$ khoảng cách giữa d' và (P) bằng độ dài h của đường vuông góc chung của d' và d.
và d thì $d' \parallel (P) \Rightarrow$ khoảng cách giữa d' và (P) bằng độ dài h của đường vuông góc chung của d' và d.
Trên ![]() ta lấy điểm D' sao cho $AD'=CD=b$.
ta lấy điểm D' sao cho $AD'=CD=b$.
Nếu gọi ![]() là góc giữa hai đường thẳng d và d' thì $\widehat{D'AB}=\alpha$.
là góc giữa hai đường thẳng d và d' thì $\widehat{D'AB}=\alpha$.
Do ![]() nên $V_{ABCD}=V_{ABCD'}$.
nên $V_{ABCD}=V_{ABCD'}$.
Mặt khác có ![]() .
.
Do d và d' cố định nên ![]() là không đổi nên $V_{ABCD}$ không đổi.
là không đổi nên $V_{ABCD}$ không đổi.
Xem thêm bài viết khác
- Giải câu 4 bài: Phương trình đường thẳng trong không gian
- Giải câu 3 bài: Khối đa diện lồi và khối đa diện đều
- Giải câu 8 bài: Phương trình mặt phẳng
- Giải câu 8 bài: Khái niệm về mặt tròn xoay
- Giải câu 3 bài: Khái niệm về khối đa diện
- Dạng 1: Phương trình mặt phẳng (P) đi qua 1 điểm và biết VTPT hoặc cặp VTCP
- Dạng 4: Viết phương trình đường thẳng d đi qua điểm A, vuông góc với đường thẳng $d_{1}$ và cắt đường thẳng $d_{2}$
- Giải câu 10 bài: Ôn tập chương I: Khối đa diện
- Giải câu 4 bài: Mặt cầu
- Giải câu 7 bài: Khái niệm về mặt tròn xoay
- Giải câu 1 bài: Khái niệm về khối đa diện
- Giải câu 4 bài: Khái niệm về khối đa diện











