-
Tất cả
-
 Tài liệu hay
Tài liệu hay
-
 Toán Học
Toán Học
-
 Soạn Văn
Soạn Văn
-
Soạn đầy đủ
- Tiếng Việt 2 tập 2 KNTT
- Tiếng Việt 2 CTST
- Tiếng Việt 2 sách Cánh Diều
- Tiếng Việt 3 tập 2
- Tiếng Việt 3 tập 1
- Tiếng Việt 4 tập 2
- Tiếng Việt 4 tập 1
- Tiếng Việt 5 tập 2
- Tiếng Việt 5 tập 1
- Soạn văn 6
- Soạn văn 7
- Soạn văn 8 tập 1
- Soạn văn 8 tập 2
- Soạn văn 9 tâp 1
- Soạn văn 9 tập 2
- Soạn văn 10 tập 1
- Soạn văn 10 tập 2
- Soạn văn 11
- Soạn văn 12
-
Soạn ngắn gọn
- Soạn văn 12 ngắn gọn tập 1
- Soạn văn 12 ngắn gọn tập 2
- Soạn văn 11 ngắn gọn tập 1
- Soạn văn 11 ngắn gọn tập 2
- Soạn văn 10 ngắn gọn tập 1
- Soạn văn 10 ngắn gọn tập 2
- Soạn văn 9 ngắn gọn tập 1
- Soạn văn 9 ngắn gọn tập 2
- Soạn văn 8 ngắn gọn tập 1
- Soạn văn 8 ngắn gọn tập 2
- Soạn văn 7 ngắn gọn tập 1
- Soạn văn 7 ngắn gọn tập 2
- Ngữ văn VNEN
- Đề thi THPT QG môn Ngữ Văn
-
Soạn đầy đủ
-
 Tiếng Anh
Tiếng Anh
-
 Vật Lý
Vật Lý
-
 Hóa Học
Hóa Học
-
 Sinh Học
Sinh Học
-
 Lịch Sử
Lịch Sử
-
 Địa Lý
Địa Lý
-
 GDCD
GDCD
-
 Khoa Học Tự Nhiên
Khoa Học Tự Nhiên
-
 Khoa Học Xã Hội
Khoa Học Xã Hội
-
Giải câu 3 bài: Khái niệm về mặt tròn xoay
Câu 3: Trang 39 - sgk hình học 12
Một hình nón có đường cao h = 20cm, bán kính đáy r = 25cm.
a) Tính diện tích xung quanh của hình nón đã cho.
b) Tính thể tích của khối nón được tạo thành bởi hình nón đó.
c) Một thiết diện đi qua đỉnh của hình nón và khoảng cách từ tâm của đáy đến mặt phẳng thiết diện là 12cm. Tính diện tích thiết diện đó.
Bài làm:
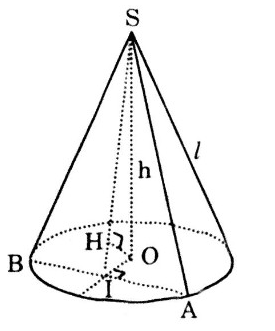
a) Giả sử SA = l là độ dài đường sinh, SH = h là chiều cao hình nón.
Trong tam giác vuông SOA ta có:
$SA^{2}=SO^{2}+OA^{2}=h^{2}+r^{2}=20^{2}+25^{2}=1025
=> ![]()
Diện tích xung quanh hình nón là:
![]()
b) Thể tích khối nón là:
![]()
c) Giả sử thiết diện SAB đi qua đỉnh S cắt đường tròn đáy tại A và B. Gọi I là trung điểm cỉa dây cung AB. Từ tâm O của đáy vẽ OH vuông góc với SI.
Ta có: ![]()
=> ![]()
Mà: ![]()
<=> ![]()
Xét tam giác vuông SOI, có: ![]()
=> ![]()
<=> ![]()
<=> ![]()
Xét tam giác vuông AOI, có: ![]()
=> ![]()
Mặt khác: ![]()
<=> ![]()
=> Diện tích thiết diện SAB là: ![]()
Xem thêm bài viết khác
- Giải câu 4 bài: Phương trình đường thẳng trong không gian
- Dạng 2: VIết phương trình mặt phẳng (P) đi qua một điểm M và song song với mặt phẳng (Q).
- Giải câu 5 bài: Ôn tập chương I: Khối đa diện
- Giải câu 7 bài: Ôn tập chương I: Khối đa diện
- Giải câu 1 bài: Khái niệm về thể tích của khối đa diện
- Giải câu 3 bài: Phương trình mặt phẳng
- Giải câu 10 bài: Mặt cầu
- Giải câu 6 bài: Ôn tập chương I: Khối đa diện
- Giải câu 9 bài: Khái niệm về mặt tròn xoay
- Giải bài 1: Khái niệm về mặt tròn xoay
- Giải câu 10 bài: Phương trình mặt phẳng
- Dạng 1: Khối lăng trụ có góc giữa đường thẳng và mặt phẳng.











