Giải câu 3 bài: Khối đa diện lồi và khối đa diện đều

Bài 3: Trang 18 - sgk hình học 12

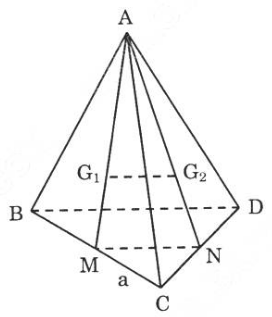
Chứng minh rằng tâm của các mặt của hình tứ diện đều là các đỉnh của một tứ diện đều.

Bài làm:

Gọi $G_{1}, G_{2}, G_{3}, G_{4}$ theo thứ tự là tâm của các mặt ABC, ACD, ABD, BCD.

Gọi M là trung điểm của BC và N là trung điểm của CD.

Vì tam giác ABC và ACD là tam giác đều nên $G_{1}, G_{2}$ theo thứ tự là trọng tâm của tam giác ABC và ACD. Ta có

$\frac{AG_{1}}{AM}=\frac{AG_{2}}{AN}=\frac{2}{3}$

Theo định lý Talet trong mặt phẳng, ta có $G_{1}G_{2} \parallel MN$ và suy ra

$G_{1}G_{2}=\frac{2}{3}MN \Rightarrow G_{1}G_{2}=\frac{a}{3}$ (vì $MN=\frac{1}{2}a$).

Tương tự ta tính được $G_{1}G_{2}=G_{1}G_{3}=G_{2}G_{3}=G_{2}G_{4}=G_{3}G_{4}$ .

Vậy $G_{1}G_{2}G_{3}G_{4}$ là tứ diện đều.

Cập nhật: 07/09/2021

Xem thêm bài viết khác