Giải câu 5 bài: Khái niệm về thể tích của khối đa diện

1 Đánh giá

Bài 5: Trang 26 - sgk hình học 12

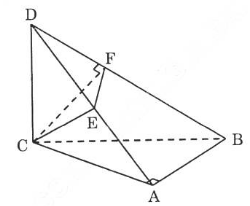
Cho tam giác ABC vuông cân ở A và AB=a. Trên đường thẳng qua C và vuông góc với mặt phẳng (ABC) lấy điểm D sao cho CD=a. Mặt phẳng qua C vuông góc với BD, cắt BD tại F và cắt AD tại E. Tính thể tích khối tứ diện CDEF theo a.

Bài làm:

Hướng dẫn vẽ hình: Tam giác ABC vuông cân tại A nhưng ta có thể vẽ tam giác thường cũng được sao cho cạnh dài nhất nằm ở bên trong (ở đây là BC). Sau đó từ C, ta dựng đường thẳng đứng vuông góc lên và lấy điểm D trên đó.

Mặt phẳng qua C vuông góc với BD cắt BD tại F và cắt CD tại E tức là từ C kẻ $CF \perp BD$ , từ F dựng đường thẳng vuông góc với BD cắt DA tại E hay $EF \perp DB \Rightarrow (CEF)\perp DB$.

Giải:

Xét tam giác DCB vuông tại C có

$DB=\sqrt{DC^{2}+CB^{2}}=\sqrt{DC^{2}+AC^{2}+AB^{2}}=\sqrt{3}a$

$DF.DB=CD^{2} \Rightarrow \frac{DF}{DB}=\frac{CD^{2}}{DB^{2}}=\frac{a^{2}}{3a^{2}}=\frac{1}{3}$ .

$\left.\begin{matrix} DC \perp AB\\ CA \perp AB\end{matrix}\right\} \Rightarrow AB \perp (DAC) \Rightarrow AB \perp CE$ .

Hơn nữa ta có $CE \perp BD$ (do $(CEF) \perp BD)$) $\Rightarrow CE\perp (DAB) \Rightarrow CE \perp DA$.

Tam giác DCA vuông cân tại đỉnh C mà $CE \perp DA$ nên E là trung điểm của DA.

$\Rightarrow \frac{DE}{DA}=\frac{1}{2}$ .

Áp dụng công thức tỉ số thể tích ta có

$\frac{V_{CDEF}}{V_{ABCD}}=\frac{DC}{DC}.\frac{DE}{DA}.\frac{DF}{DB}=\frac{1}{2}.\frac{1}{3}=\frac{1}{6}$ .

Mà $V_{DABC}=\frac{1}{3}.DC. S_{ABC}=\frac{1}{3}.a.\frac{1}{2}.a^{2}=\frac{a^{3}}{6}$

$\Rightarrow V_{DECF}=\frac{a^{3}}{36}$ (dvtt).

4 lượt xem

Cập nhật: 07/09/2021

Xem thêm bài viết khác

Xem thêm Hình học 12