Dạng 5: Khối chóp và phương pháp tỉ số thể tích
Dạng 5: Khối chóp và phương pháp tỉ số thể tích
Bài làm:
I.Phương pháp giải
muốn tính thể tích khối chóp con trong khối chóp to, ta tính tỉ lệ các cạnh bên tương ứng của hai khối chóp. Từ đó suy ra được tỷ số thể tích.
II.Bài tập vận dụng
Bài tập 1: Cho hình chóp S.ABC có tam giác ABC vuông cân ở B, AC = ![]() ,SA vuông góc với đáy ABC , SA = a. Gọi G là trọng tâm tam giác ABC, mặt phẳng (m) qua AG và song song với BC cắt SC, SB lần lượt tại M, N. Tính thể tích của khối chóp S.AMN.
,SA vuông góc với đáy ABC , SA = a. Gọi G là trọng tâm tam giác ABC, mặt phẳng (m) qua AG và song song với BC cắt SC, SB lần lượt tại M, N. Tính thể tích của khối chóp S.AMN.
Bài giải:
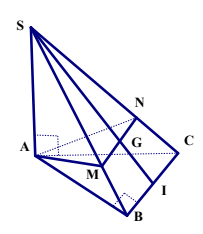
Ta có ![]() vuông cân tại B, AC = $a\sqrt{2}$ suy ra AB = BC = a.
vuông cân tại B, AC = $a\sqrt{2}$ suy ra AB = BC = a.
![]() .
.
Có: ![]()
Gọi I là trung điểm của đoạn thẳng BC. G là trọng tâm của tam giác ![]() .
.
Mặt phẳng (m) qua AG và song song với BC cắt SC, SB lần lượt tại M, N.
![]()
Vậy ta có: ![]()
![]() .
.
Bài tập 2: Cho khối tứ giác đều SABCD. Một mặt phẳng (m) qua A, B và trung điểm M của SC. Tính tỉ số thể tích của hai phần khối chóp bị phân chia bởi mặt phẳng đó.
Bài giải:
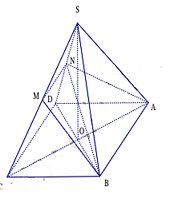
Ta kẻ MN // CD ( N thuộc SD)SD) thì hình thang ABMN là thiết diện của khối chóp khi cắt bởi mặt phẳng (ABM).
Ta có: ![]() .
.
![]()
![]()
Mà ![]()
![]()
![]()
Xem thêm bài viết khác
- Dạng 3: Viết phương trình hình chiếu của đường thẳng (d) lên mặt phẳng (P).
- Giải câu 1 bài: Khái niệm về khối đa diện
- Giải câu 10 bài: Phương trình mặt phẳng
- Giải câu 10 bài: Phương trình đường thẳng trong không gian
- Giải câu 6 bài: Mặt cầu
- Giải câu 6 bài: Phương trình đường thẳng trong không gian
- Giải câu 1 bài: Phương trình mặt phẳng
- Giải câu 12 bài: Ôn tập chương I: Khối đa diện
- Dạng 1: Vết phương trình đường thẳng d đi qua A và vuông góc với hai đường thẳng $d_{1}$ và $d_{2}$.
- Giải câu 2 bài: Hệ tọa độ trong không gian
- Giải câu 10 bài: Mặt cầu
- Giải câu 8 bài: Phương trình mặt phẳng











