Dạng 1: Khối lăng trụ có góc giữa đường thẳng và mặt phẳng.

Phần tham khảo mở rộng

Dạng 1: Khối lăng trụ có góc giữa đường thẳng và mặt phẳng.

Bài làm:

I.Phương pháp giải

Từ góc giữa đường thẳng và mặt phẳng ta tìm được chiều cao và các cạnh tương ứng để tính diện tích mặt đáy. Qua đó tìm được thể tích khối lăng trụ.

II.Bài tập vận dụng

Bài tập 1: Cho lăng trụ đứng tam giác có đáy ABC là tam giác vuông cân tại B với BA = BC = a, biết $A^{'}B$ hợp với đáy ABC một góc $60^{\circ}$. Tính thể tích lăng trụ.

Bài giải:

Ta có: và AB là hình chiếu của AB trên (ABC).

Do đó

Xét tam giác vuông tại A có: $A^{'}A = AB.tan60^{\circ}$=$a\sqrt{3}$.

.

Vậy .

Bài tập 2: Cho lăng trụ đứng có đáy ABCD là hình vuông cạnh a, đường chéo $BD^{'}$ hợp với đáy ABCD một góc $30^{\circ}$. Tính thể tích của lăng trụ.

Bài giải:

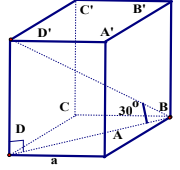
nên ta có $DD^{'}\perp (ABCD)\Rightarrow DD^{'}\perp BD$ và BD là hình chiếu của $BD^{'}$ trên $(ABCD)$.

Do đó :

Xét tam giác vuông tại D: $DD^{'}=BD.tan30^{\circ}$=$\frac{a\sqrt{6}}{3}$

Vậy