Giải câu 42 bài: Ôn tập chương II sgk Toán hình 9 tập 1 Trang 128

Câu 42: Trang 128 - sgk toán 9 tập 1

Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A, BC là tiếp tuyến chung ngoài. B ∈ (O), C ∈ (O’). Tiếp tuyến chung trong tại A cắt BC ở điểm M. Gọi E là giao điểm của OM và AB, F là giao điểm của O’M và AC. Chứng minh rằng :

a. Tứ giác AEMF là hình chữ nhật.

b. ME.MO = MF.MO’ .

c. OO’ là tiếp tuyến của đường tròn có đường kính là BC.

d. BC là tiếp tuyến của đường tròn có đường kính là OO’.

Bài làm:

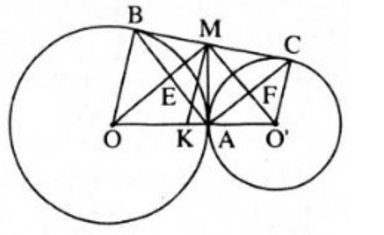
a. Ta có : MA, MB là các tiếp tuyến của đường tròn (O) (gt).

Theo tính chất của hai tiếp tuyến cắt nhau, ta có :

• MA = MB
• MO là tia phân giác góc AMB.

Xét ∆MAB cân tại M (MA = MB)

Có MO là đường phân giác nên đồng thời là đường cao .

=>

Chứng minh tương tự có MO’ là tia phân giác góc AMC và góc .

Vì : MO, MO’ là tia phân giác của hai góc kẻ bù

=>

Xét tứ giác AEMF có :

=> Tứ giác AEMF là hình chữ nhật . ( đpcm )

b. Xét ∆MAO vuông tại A có : AE là đường cao

=>

Tương tự, ta có:

=> ( đpcm )

c. Ta có MA = MB = MC nên M là tâm đường tròn đường kính BC có bán kính là MA.

Mà tại A.

=> OO’ là tiếp tuyến của đường tròn đường kính BC . ( đpcm )

d. Gọi K là trung điểm OO’, ta có K là tâm đường tròn có đướng kính là OO’, bán kính KM (∆MOO’ vuông tại M)

Ta có :

=> Tứ giác OBCO’ là hình thang có K, M lần lượt là trung điểm các cạnh cạnh bên OO’, BC.

Do đó KM là đường trung bình của hình thang OBCO’ => KM // OB

Mà tại M

=> BC là tiếp tuyến của đường tròn đường kính OO' . ( đpcm )