Giải câu 61 bài 9: Hình chữ nhật sgk Toán hình 8 tập 1 Trang 99

Câu 61 : Trang 99 sgk toán 8 tập 1

Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC, E là điểm đối xứng với H qua I. Tứ giác AHCE là hình gì ? Vì sao ?

Bài làm:

Theo giả thiết ta có hình vẽ sau:

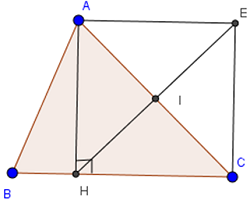
Ta có: I là trung điểm của AC => IA = IC

Mặt khác ta có E là điểm đối xứng với H qua I => IH = IE

=>I là giao của AC và HE và là trung điểm của mỗi đường

=> AHCE là hình bình hành. (1)

Do AH là đường cao của tam giác ABC=> AH vuông góc với BC

=> = 90⁰ (2)

Từ (1) và (2) ta thấy tứ giác AHCE là hình bình hành có một góc vuông

=> tứ giác AHCE là hình chữ nhật.